自动控制原理课本 3-6线性系统的稳态误差计算

1.误差与稳态误差

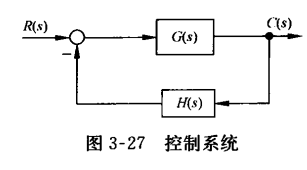
设控制系统结构图如图3-27所示。当输入信号$R(s)$与主反馈信号$B(s)$不相等时,比较装置的输出为:
$E(s)=R(s)-H(s)C(s)\quad (3-69)$
此时,系统在$E(s)$信号作用下产生动作,使输出量趋于希望值。通常,称$E(s)$为误差信号,简称误差(亦称偏差)。
……

误差本身是时间的函数,其时域表达式为
$e(t)=L^{-1}[E(s)]=L^{-1}[\varPhi(s)R(s)]$
式中，$\varPhi(s)$为系统误差传递函数，由下面的式子决定:
$\varPhi(s)=\dfrac{E(s)}{R(s)}=\dfrac{1}{1+G(s)H(s)}$
在误差信号$e(t)$中,包含瞬态分量$e_{ts}(t)$和稳态分量$e_{ss}(t)$两部分。由于系统必须稳定,故当时间趋于无穷时,必有$e_{ts}(t)$趋于零。

稳态误差定义

因此,控制系统的稳态误差定义为误差信号$e(t)$的稳态分量$e_ss(\infty)$,常以$e_ss$简单标志
如果有理函数$sE(s)$除在原点处有唯一的极点外,在$s$右半平面及虚轴上解析,即$sE(s)$的极点均位于$s$左半平面(包括坐标原点),则可根据拉氏变换的终值定理,由式(3-72)方便地求出系统的稳态误差:
$e_{ss}(\infty)=\lim \limits_{s \to 0}E(s)=\lim \limits_{s \to 0}\dfrac{sR(s)}{1+G(s)H(s)}$
由于上式算出的稳态误差是误差信号稳态分量$e_{ss}(t)$在$t$趋于无穷时的数值,故有时称之为$t$,它不能反映$e_{ss}(\infty)$随时间$t$的变化规律,具有一定的局限性。

例3-12

例3-12设单位反馈系统的开环传递函数为$G(s)=\dfrac{1}{Ts}$,输入信号分别为$r(t)=t^2/2$以及$r(t)=\sin\omega t$,试求控制系统的稳态误差。

解

$L[\dfrac{1}{2} t^2]=\dfrac{1}{s^3}$,

当 $r(t)=\dfrac{t^2}{2}$时，$R(s)=\dfrac{1}{t^3}$
由$\varPhi(s)=\dfrac{E(s)}{R(s)}=\dfrac{1}{1+G(s)H(s)}$,可得:
$E(s)=\dfrac{R(s)}{1+G(s)H(s)}$
代入$R(s)=\dfrac{1}{t^3}$，$G(s)=\dfrac{1}{Ts}$，$H(s)=1$(单位反馈),得:
$$
\begin{aligned}
E(s)=&\dfrac{R(s)}{1+G(s)H(s)} \\
=&\dfrac{\dfrac{1}{s^3}}{1+\dfrac{1}{Ts}\times 1} \\
=&\dfrac{\dfrac{1}{s^3}(Ts(s^3))}{Ts(s^3)\times 1+\dfrac{1}{Ts}\times Ts(s^3)} \\
=&\dfrac{Ts}{Ts(s^3)+s^3} \\
=&\dfrac{T}{Ts^3+s^2} \\
=&\dfrac{1}{s^3+s^2\dfrac{1}{T}} \\
=&\dfrac{1}{s^2(s+\dfrac{1}{T})} \\
\end{aligned}
$$
化为部分分式之和的形式(展开过程：
$\begin{aligned} E(s)=&\dfrac{A}{s^2}+\dfrac{B}{s}+\dfrac{C}{s+\dfrac{1}{T}} \\ =&\dfrac{T}{s^2}-\dfrac{T^2}{s}+\dfrac{T^2}{s+\dfrac{1}{T}} \\ \end{aligned}$
剩下的我看不懂…先这样吧,继续往下看.

2.系统类型

由稳态误差计算通式$e_{ss}(\infty)=\lim \limits_{s \to 0}E(s)=\lim \limits_{s \to 0}\dfrac{sR(s)}{1+G(s)H(s)}$可见,控制系统稳态误差数值,与开环传递函数$G(s)H(s)$的结构和输人信号$R(s)$的形式密切相关。对于一个给定的稳定系统,当输入信号形式一定时,系统是否存在稳态误差就取决于开环传递函数描述的系统结构。因此,按照控制系统跟踪不同输入信号的能力来进行系统分类是必要的。
在一般情况下,分子阶次为$m$,分母阶次为$n$的开环传递函数可表示为:

原文链接: 自动控制原理课本 3-6线性系统的稳态误差计算