测验1

题1-1

极限存在而且等于函数值则连续
所以连续能推出极限存在(充分条件)，而极限存在不能推出连续(非必要条件)

题1-2

特殊角的三角函数值表
$x \to 0$时等价无穷小公式:
$ln(1+x) \sim x$
$\sqrt[n]{1+x}-1 \sim \dfrac{1}{n}x$
解:$f(0)=cos(\dfrac{\pi}{3}0)-\dfrac{1}{3}0=1-0=1$
$f(0)=cos(\dfrac{\pi}{3}1)-\dfrac{1}{3}1=\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1}{6}$
$\lim \limits_{x \to 0^- }\dfrac{ln(1+ax)}{x}=\lim \limits_{x \to 0^- }\dfrac{ax}{x}=a=f(0)=1$

令$u=x-1$,则$x \to 1$时，有$u \to 0$
$ \sqrt{x}-1= \sqrt{1+(x-1)}-1 = \sqrt{1+u}-1 \sim u $
$\lim \limits_{x \to 1 }\dfrac{\sqrt{x}-1}{x^3-b}
=\lim \limits_{x \to 1 }\dfrac{(x-1)}{x^3-b}$
当b=1时，上式等于:
$$
\begin{align}
&\lim \limits_{x \to 1 }\dfrac{(x-1)}{x^3-b} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(x-1)}{x^3-1} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(x-1)}{(x-1)(x^2+x\times 1+x^2)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{1}{(x^2+x\times 1+x^2)} \nonumber \\
=&\dfrac{1}{3} \nonumber \\
\ne& f(1) \nonumber \\
=&\dfrac{1}{6} \nonumber \\
\end{align}
$$
当$b=\dfrac{1}{2}$时，
$\lim \limits_{x \to 1 }\dfrac{(x-1)}{x^3-b}
=\lim \limits_{x \to 1 }\dfrac{(x-1)}{x^3-\dfrac{1}{2}}
=f(0)
=2
$

题1-3

解:
$x \to 0$时，有等价无穷小公式:
$e^x-1 \sim x$
$f(0)=0^2-2=2$
$\lim \limits_{x \to 0 }\dfrac{e^{ax}-1}{x}
=\lim \limits_{x \to 0 }\dfrac{ax}{x}
=a
$

题1-4

$\lim \limits_{x \to 0 }x=0$,$\left| cos\dfrac{2}{x} \right|\le 1$,所以
$\lim \limits_{x \to 0 }x cos\dfrac{2}{x}=0$
所以$\lim \limits_{x \to 0 }x cos\dfrac{2}{x}+x^2=0$
左右极限存在,是第一类间断点，左右极限相等,是可去间断点

题1-5

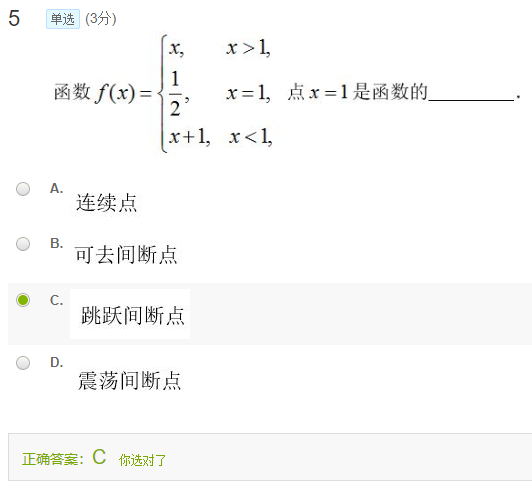
$f(1)=\dfrac{1}{2}$
$\lim \limits_{x \to 1^+ }f(x)=\lim \limits_{x \to 1^+ }x=1$
$\lim \limits_{x \to 1^- }f(x)=\lim \limits_{x \to 1^+ }x-1=0$
左右极限都存在，所以是第一类间断点。排除震荡间断点。
左右极限存在，但是不相等，所以是跳跃间断点。

题1-6

$f(0)=a\times 0+b=b$
$f(1)=a\times 1+b=a+b$
$x \to 0$时,有等价无穷小:
$\sqrt{1+x}-1 \sim x$
$
\lim \limits_{x \to 0^- }\dfrac{ \sqrt{1+x}-1}{x}
=\lim \limits_{x \to 0^- }\dfrac{x}{x}
=1
=f(0)
=b
$
因为$x \to 1$时,$x-1$为无穷小
$\lim \limits_{x \to 1^+ } \sqrt{x}+1=2=f(1)=a+b=a+1$
所以$a=1$

题1-7

解:
$\lim \limits_{x \to 2^- }f(x)=\lim \limits_{x \to 2^- }ax+b=2a+b=f(2)=1$
$$
\begin{align}
&\lim \limits_{x \to 2^+ }f(x) \nonumber \\
=&\lim \limits_{x \to 2^+ } \dfrac{\sqrt{ax}-\sqrt{2a}}{x-2} \nonumber \\
=&\lim \limits_{x \to 2^+ } \dfrac{\sqrt{a}(\sqrt{x}-\sqrt{2})}{x-2} \nonumber \\
=&\lim \limits_{x \to 2^+ } \dfrac{\sqrt{a}(\sqrt{x}-\sqrt{2})}{(\sqrt{x}- \sqrt{2})(\sqrt{x}+\sqrt{2})} \nonumber \\
=&\lim \limits_{x \to 2^+ } \dfrac{\sqrt{a}}{\sqrt{x}+\sqrt{2}} \nonumber \\
=&\dfrac{\sqrt{a}}{\sqrt{2}+\sqrt{2}} \nonumber \\
=&\dfrac{\sqrt{a}}{2\sqrt{2}} \nonumber \\
=&f(2) \nonumber \\
=&1 \nonumber \\
\end{align}
$$
所以$\sqrt{a}=2\sqrt{2}$,$a=4\times 2=8$,又由$2a+b=f(2)=1$,所以$b=1-2a=1-2\times 6=-15$