自动控制原理NJUPT MOOC作业题3
第1题
题目:(作业题3-4):
知识点窍:二阶系统的动态性能指标。
逻辑推理:由二阶系统单位阶跃响应的表达式与标准单位阶跃响应的表达式相比较,求出此二阶系统的各动态性能指标
解题过程
$$
\begin{aligned}
h(t)=&10-12.5e^{-1.2t}sin(1.6t+53.1°) \\
=&10[1-1.25e^{-1.2t}sin(1.6t+53.1°)] \\
\end{aligned}
$$
由上式可得,此二阶系统的放大系数是$10$,但放大系数并不影响系统的动态性能指标。
由于标准的二阶系统单位阶跃响应表达式为(课本73页):
$$h(t)=1-\dfrac{1}{\sqrt{1-\zeta^2}}e^{-\zeta\omega_nt}sin(\omega_n\sqrt{1-\zeta^2}t+\beta)$$
所以有:
$$
\begin{cases}
\zeta\omega_n=1.2 \\
\dfrac{1}{\sqrt{1-\zeta^2}}=1.25 \\
\omega_n\sqrt{1-\zeta^2}=1.6
\end{cases}
$$
解得:
$$
\begin{cases}
\zeta=0.6 \\
\omega_n=2
\end{cases}
$$
因为$0<\zeta<1$。所以,此系统为欠阻尼二阶系统,其动态性能指标如下:
超调量(公式在课本76页面):
$$
\begin{aligned}
\sigma\%=&e^{\dfrac{-\pi\zeta}{\sqrt{1-\zeta^2}}}\times 100\% \\
=&e^{-0.6\times1.25\pi}\times100\% \\
\approx&9.5\% \\
\end{aligned}
$$
峰值时间:
$$t_p=\dfrac{\pi}{\omega_d}=\dfrac{\pi}{\omega_n\sqrt{1-\zeta^2}}=\dfrac{\pi}{2\times0.8}\approx19.6s$$
调节时间:
$$
t_s=\dfrac{3.5}{\zeta\omega_n}=\dfrac{3.5}{2\times0.6}=2.92s
$$
第2题
新作业答案题3-7
设单位负反馈系统的开环传递函数为,试应用劳斯稳定判据确定义为多大值时,特使系统振荡,并求出振荡频率。
由题得,特征方程为:$s^4+12s^3+69s^2+198s+200+K=0$
列劳斯表如下所示:
| $s^4$ | $1$ | $69$ | $200+K$ |
| $s^3$ | $12$ | $198$ | |
| $s^2$ | $52.5$ | $200+K$ | |
| $s^1$ | $7995-12K$ | ||
| $s^0$ | $200+K$ |
根据题意,令$s^1$所在的行全部为$0$,即$7995-12K=0$,解得:$K=666.25$
由$s^2$行可得:$52.5s^2+200+666.25=0$,解得:$s=\pm4.062i$,
所以振荡角频率为$\omega=4.062rad/s$
第3题
课后习题3-15第二小题,第二小问
3-15已知单位反馈系统的开环传递函数分别为:
$$
G(s)=\dfrac{50}{s(0.1s+1)(s+5)}
$$
试求输入为$r(t)=2+2t+t^2$时,系统的稳态误差。
考察知识
知识点窍:稳态误差、静态误差系统法、终值定理
逻辑推理:根据线性叠加原理,用静态误差系数法或终值定理来求系统的稳态误差。
如何判断是几型系统
$\begin{aligned} G(s)H(s)=&\dfrac{K(1+\tau_1s)(1+\tau_2s)\cdots(1+\tau_ms)}{s^v(1+T_1s)(1+T_2s)\cdots(1+T_{n-v}s)} \\ =&\dfrac{K\prod\limits_{j=1}^{m}(\tau_js+1)}{s^v\prod\limits_{i=1}^{n-v}(T_is+1)} \\ \end{aligned}$
当$v=0$时,称该系统为0型系统
当$v=1$时,称该系统为1型系统
当$v=2$时,称该系统为2型系统
不同输入信号下的稳态误差表
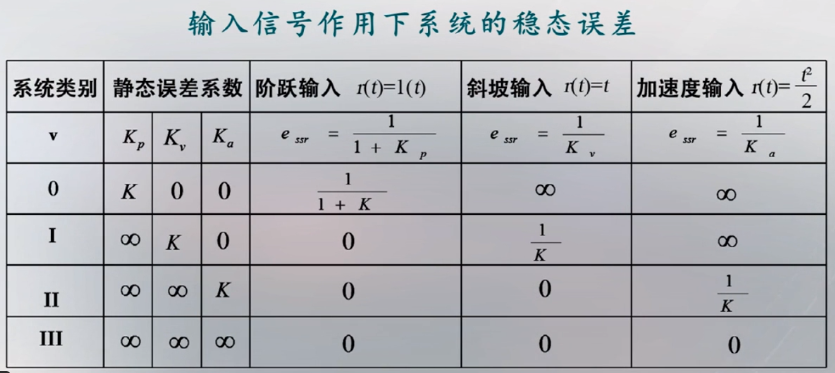
解
$$
G(s)=\dfrac{50}{s(0.1s+1)(s+5)}=\dfrac{10}{s(0.1s+1)(0.2s+1)}
$$
由上式可知$v=1$,该系统是$1$型系统,且$K=10$。
$1$型系统在$1(t),t,\dfrac{1}{2}t^2$信号作用下的稳态误差分别为:$0,\dfrac{1}{K},\infty$根据线性叠加原理,该系统在输入为$r(t)=2+2t+t^2$时的稳态误差为:
$e_{ss}=2\times 0+2\times \dfrac{1}{K}+\infty=\infty$
第4题
第五版答案3-15
另一个答案3-1
假设温度计可用$\dfrac{1}{Ts+1}$传递函数描述其特性,现在用温度计测量盛在容器内的水温。发现需要$1min$时间才能指示出实际水温的$98\%$的数值,试问该温度计指示出实际水温从$10\%$变化到$90\%$所需的时间是多少?
相关知识点
室温调节系统、恒温箱以及水位调节系统的闭环传递函数形式:
$\varPhi(s)=\dfrac{C(s)}{R(s)}=\dfrac{1}{Ts+1}$
一阶系统的单位阶跃响应为$c(t)=1-e^{\dfrac{-t}{T}}$
可用时间常数$T$去度量系统输出量的数值。例如,当$t=T$时,$c(T)=0.632$;而当t分别等于$2T,3T$和$4T$时,$c(t)$的数值将分别等于终值的$86.5\%$,$95\%$和$98.2\%$。根据这一特点,可用实验方法测定一阶系统的时间常数,或判定所测系统是否属于一阶系统。
根据动态性能指标的定义,一阶系统的动态性能指标为:
$t_r=2.20T$,$t_s=3T(\Delta=5\%)$或$t_s=4T(\Delta=2\%)$
上升时间$t_r$,指响应从终值$10\%$上升到终值$90\%$所需的时间;对于有振荡的系统,亦可定义为响应从零第一次上升到终值所需的时间。上升时间是系统响应速度的一种度量。上升时间越短,响应速度越快
解:
水温从$0\%$上升到$98\%$的时间为调节时间$t_s$,一阶系统的动态性能指标$t_s=4T$
水温从$10\%$变化到$90\%$所需的时间为上升时间$t_r$
一阶系统的单位阶跃响应为$c(t)=1-e^{\dfrac{-t}{T}}$
$t_s=4T=1min$,解得:$T=0.25min$,设水温变化函数为$h(t)$,则$h(t)=1-e^{\dfrac{-t}{T}}$
$h(t_1)=1-e^{\dfrac{-t}{T}}=0.1$,解得$t_1=-Tln0.9$
$h(t_1)=1-e^{\dfrac{-t}{T}}=0.9$,得到:$t_2=-Tln0.1$
所以$t_r=t_2-t_1=Tln\dfrac{0.9}{0.1}=2.2T=0.55min$
原文链接: null

