自动控制原理作业题 2-22

2-22试用梅森增益公式求图2-59中各系统信号流图的传递函数$C(s)/R(s)$。

图a

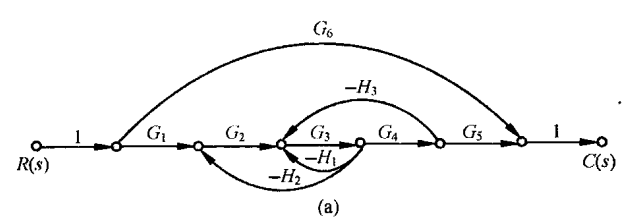
图b

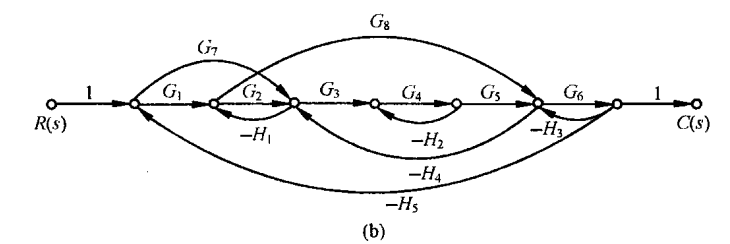
图c

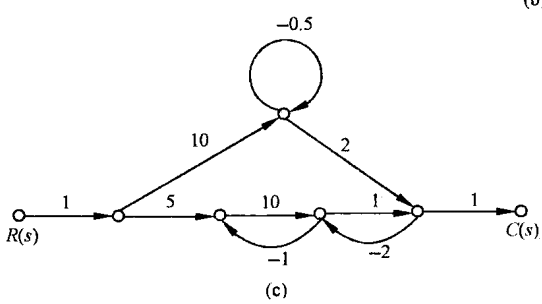
图d

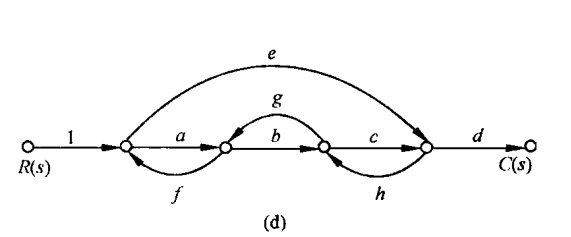
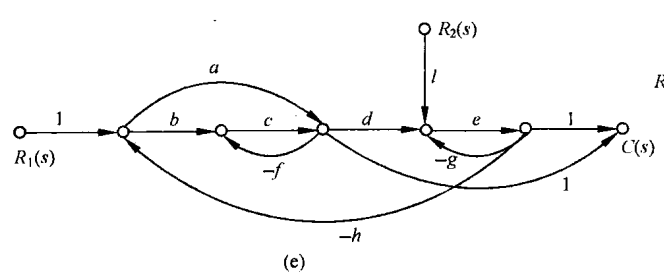
图e

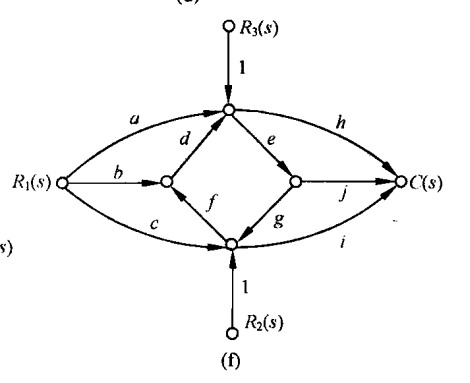
图f

考点

知识点窍：梅森增益公式。
逻辑推理：根据信号流图利用梅森增益公式求系统的传递函数

解题过程

图a

为了便于分析,在信号流图中标出节点，如下图所示: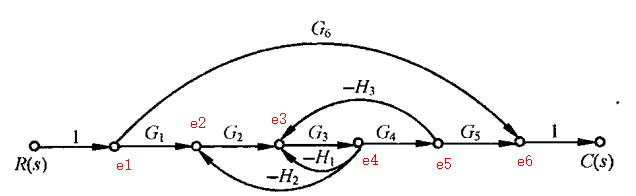

图b

为了便于分析，在信号流图中标出节点，如下图所示: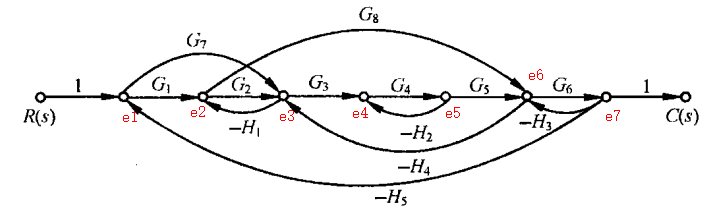

这题好变态啊
有九条单独回路：

有六组互不接触回路,一个三三互不接触回路: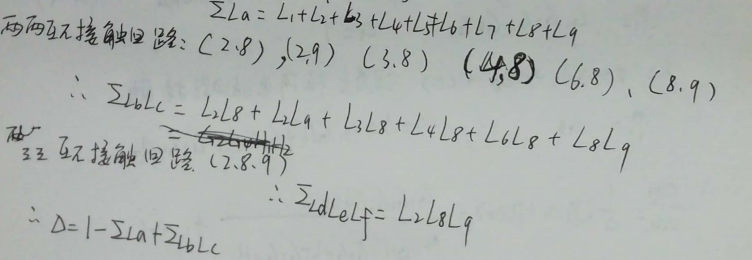

$L_1=-G_1G_2G_3G_4G_5G_6H_5$
$L_2=-G_2H_1$
$L_3=G_8H_1H_2$
$L_4=-G_1G_8G_6H_5$
$L_5=-G_3G_4G_6G_7H_5$
$L_6=G_6G_7G_8H_1H_5$
$L_7=-G_3G_4G_5H_2$
$L_8=-G_4H_2$
$L_9=-G_6H_3$
单独回路总增益：
$\sum L_a=L_1+L_2+L_3+L_4+L_5+L_6+L_7+L_8+L_9$
两两互不接触回路总增益：
$\sum L_bL_c=L_2L_8+L_2L_9+L_3L_8+L_4L_8+L_6L_8+L_8L_9$
三三互不接触回路总增益：
$\sum L_dL_eL_f=L_2L_8L_9$
所以流图特征式:
$\Delta=1-\sum L_a+\sum L_bL_c-\sum L_dL_eL_f$
前向通路：

最后代入公式,然后整理可得答案，整理略：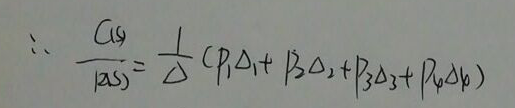

图c

为了方便分析，在信号流图中给节点命名，如下图所示：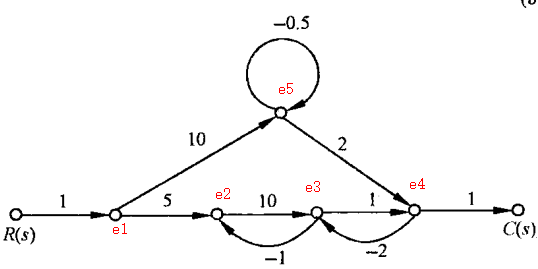

单独回路：
1:$e_2\to e_3\to e_2$,回路增益：$L_1=-10$
2:$e_3\to e_4 to e_3$,回路增益：$L_2=-2$
3:$e_5\to e_5$,回路增益：$L_3=-0.5$
两两互不接触回路 $(1,3)$,$(2,3)$
所以流图特征式:
$$
\begin{aligned}
\Delta=&1-\sum L_a+\sum L_bL_c \\
=&1-(L_1+L_2+L_3)+(L_1L_3+L_2L_3) \\
=&1+10+2+0.5+(-10)\times(-0.5)+2\times(-0.5) \\
=&19.5 \\
\end{aligned}
$$
前向通路：
1：$R(s)\to e_1\to e_2\to e_3\to e_4\to C(s)$,与回路1,回路2接触,
$p_1=50$,$\Delta_1=1+0.5=1.5$
2:$R(s)\to e_1\to e_5\to e_4\to C(s)$,与回路3,回路2,接触.
$p_2=20$,$\Delta_2=1-L_1=1+10=20$

答案

$$
\begin{aligned}
\dfrac{C(s)}{R(s)}=&\dfrac{p_1\Delta_1+p_2\Delta_2}{\Delta} \\
=&\dfrac{50\times1.5+20\times11}{19.5} \\
=& 15.128\\
\end{aligned}
$$

图d

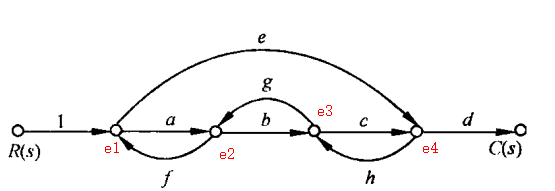
单独回路：
1：$e_1\to e_2\to e_1$,增益：$L_1=af$
2：$e_2\to e_3\to e_2$,增益：$L_2=bg$
3：$e_3\to e_4\to e_3$,增益：$L_3=ch$
4：$e_1\to e_4\to e_3\to e_2\to e_1$,增益:$L_4=efgh$
两两不接触回路：
$(L_1,L_3)$
流图特征式:
$$
\begin{aligned}
\Delta=&1-(L_1+L_2+L_3+L_4)+(L_1L_3) \\
=&1-af-bg-ch-efgh+bcgh \\
\end{aligned}
$$
前向通路：
1：$R(s)\to e_1\to e_2\to e_3\to e_4\to C(s)$,$p_1=abcd$，该前向通路与所有回路都接触，所以:
$$
\require{cancel}
\begin{aligned}
\Delta_1=&1-(\bcancel{L_1}+\bcancel{L_2}+\bcancel{L_3}+\bcancel{L_4})+\bcancel{(L_1L_3)} \\
=&1 \\
\end{aligned}
$$
1：$R(s)\to e_1\to e_4\to C(s)$,$p_2=de$,该前向通路与回路1,3,4接触，与回路2不接触,所以减去与回路1,3,4有关的增益项,得到余因子式：
$\require{cancel}
\Delta_2=1-(\bcancel{L_1}+L_2+\bcancel{L_3}+\bcancel{L_4})+\bcancel{(L_1L_3)}
=1-bg$
所以传递函数:

答案

$$
\begin{aligned}
\dfrac{C(s)}{R(s)}=&\dfrac{1}{\Delta}(p_1\Delta_1+p_2\Delta_2) \\
=&\dfrac{abcd+de(1-bg)}{1-af-bg-ch-efgh+bcgh} \\
\end{aligned}
$$

图e

解,在图中标出节点，如下图所示: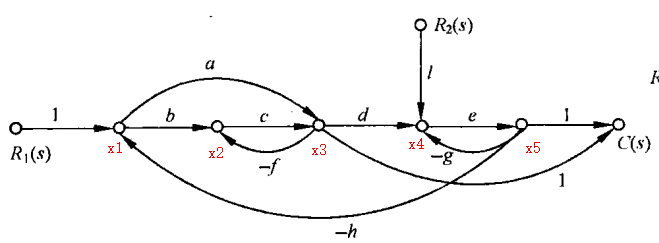

单独回路：
1:$x_1\to x_2\to x_3\to x_4\to x_5\to x_1$
增益:$L_1=-bcdeh$
2:$x_1\to x_3\to x_4\to x_5\to x_1$
增益:$L_2=-adeh$
3:$x_2\to x_3\to x_2$
增益:$L_3=-cf$
4:$x_4\to x_5\to x_4$
增益:$L_4=-eg$
两两互不接触回路:$L_3$和$L_4$
所以得到流图特征式
$$
\begin{aligned}
\Delta=&1-(L_1+L_2+L_3+L_4)+L_3L_4 \\
=&1+bcdeh+adeh+cf+eg+cefg \\
\end{aligned}
$$

R_1(s)到C(s)的前向通路：

1:$R_1(s)\to x_1\to x_2\to x_3\to x_4\to x_5\to C(s)$,
前向通路增益$p_1=bcde$
该前向通路包含所有节点,所以与所有的单独回路都接触,所以余因子式：
$$
\require{cancel}
\begin{aligned}
\Delta_1=&1-(\bcancel{L_1}+\bcancel{L_2}+\bcancel{L_3}+\bcancel{L_4})+\bcancel{L_3L_4} \\
=&1 \\
\end{aligned}
$$

2:$R_1(s)\to x_1\to x_3\to x_4\to x_5\to C(s)$,
增益：$p_2=ade$
与所有回路都接触,所以余因子式$\Delta_2=1$,
3:$R_1(s)\to x_1\to x_2\to x_3\to C(s)$
增益:$p_3=bc$,
接触单独回路$L_1,L_2,L_3$,不接触单独回路$L_4$,所以流图特征式中删去$L_1,L_2,L_3$
有关的项，保留$L_4$,即可得到余因子式:
$$
\require{cancel}
\begin{aligned}
\Delta_3=&1-(\bcancel{L_1}+\bcancel{L_2}+\bcancel{L_3}+L_4)+\bcancel{L_3L_4} \\
=&1-L_4 \\
=&1+eg \\
\end{aligned}
$$
4:$R(s)\to x_1\to x_3\to C(s)$
增益$p_4=a$
不接触回路4,接触回路1,2,3,所以余因子式:$\Delta_4=1+eg$

答案1

$$
\begin{aligned}
&\dfrac{C(s)}{R_1(s)} \\
=&\dfrac{bcde+ade+(bc+a)(1+eg)}{1+bcdeh+adeh+cf+eg+cefg} \\
\end{aligned}
$$
$R_2(s)$到$C(s)$的前向通路有:
1:$R_2(s)\to x_4\to x_5$,
增益$p_1=le$,
不接触单独回路$L_3$,所以对应的余因子式为:
$$
\require{cancel}
\begin{aligned}
\Delta_3=&1-(\bcancel{L_1}+\bcancel{L_2}+L_3+\bcancel{L_4})+\bcancel{L_3L_4} \\
=&1-L_3 \\
=&1+cf \\
\end{aligned}
$$

2:$R_2(s)\to x_4\to x_5\to x_1\to x_2\to x_3\to C(s)$
增益:$p_2=-bcehl$
接触所有回路，$\Delta_2=1$
3:$R_2(s)\to x_4\to x_5\to x_1\to x_3\to C(s)$
增益:$p_3=-aehl$
与所有回路都接触，$\Delta_3=1$

答案2

所以$R_2(s)$到$C_(s)$的传递函数为:
$$
\begin{aligned}
\dfrac{C(s)}{R_2(s)}=&\dfrac{le(1+cf)-bcehl-aehl}{1+bcdeh+adeh+cf+eg+cefg} \\
=&\dfrac{le(1+cf-bch-ah)}{1+bcdeh+adeh+cf+eg+cefg} \\
\end{aligned}
$$

图f

原文链接: 自动控制原理作业题 2-22