不定积分与导数的关系
基本积分表
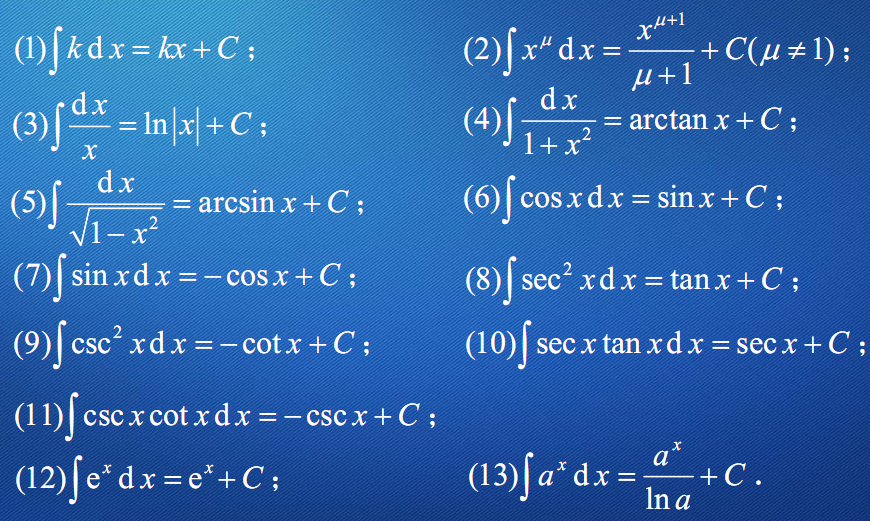
基本积分表 Latex
| 序号 | 不定积分 | 不定积分 |
|---|---|---|
| 1 | $\int kdx=kx+C$ | $\int x^udx=\dfrac{1}{u+1} x^{u+1}+C(u\ne1)$ |
| 2 | $\int a^xdx=\dfrac{a^x}{\ln a}+C$ | $\int e^xdx=e^x+C$ |
| 3 | $\int \dfrac{1}{x}dx=\ln \left\vert x \right\vert+C$ | |
| 4 | $\int \cos xdx=\sin x +C$ | $\int \sin xdx=-\cos x +C$ |
| 5 | $\int \sec^2x dx=\tan x+C$ | $\int \csc^2x dx=-\cot x+C$ |
| 6 | $\int \sec x\tan xdx=\sec x+C$ | $\int \csc x \cot xdx=-\csc x+C$ |
| 7 | $\int \dfrac{1}{\sqrt{1-x^x}}=\arcsin x +C$ | $\int -\dfrac{1}{\sqrt{1-x^x}}=\arccos x +C$ |
| 8 | $\int \dfrac{1}{1+x^2} dx=\arctan x+C$ | $\int -\dfrac{1}{1+x^2} dx=arccot x+C$ |
| 9 | $\int \dfrac{1}{a^2+x^2} dx=\dfrac{1}{a}\arctan(\dfrac{x}{a})+C$ | $\int \dfrac{1}{\sqrt{a^2-x^2}}=\arcsin(\dfrac{x}{a})+C$ |
| 10 | $\int \dfrac{1}{a^2-x^2}dx=\dfrac{1}{2a}ln \left\vert \dfrac{a+x}{a-x} \right\vert+C$ | $\int \tan x=\ln \left\vert secx \right\vert+C$ |
| 11 | $\int \cot xdx=\ln \left\vert \sin x \right\vert+C$ | $\int \csc xdx=\ln \left\vert cscx-cotx \right\vert+C$ |
| 12 | $\int \sec xdx=\ln \left\vert secx+tanx \right\vert+C$ |
不定积分的基本运算性质
性质1

性质2

简单不定积分的计算举例
例1
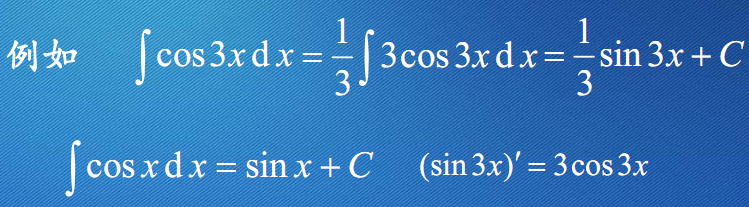
例2
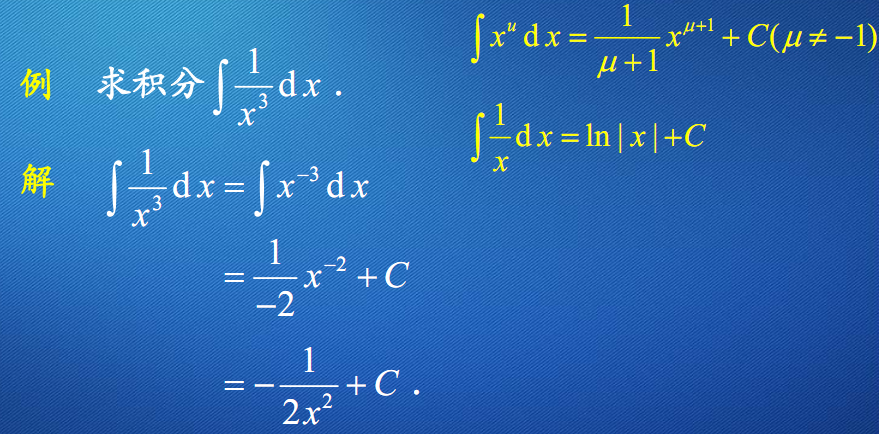
例3
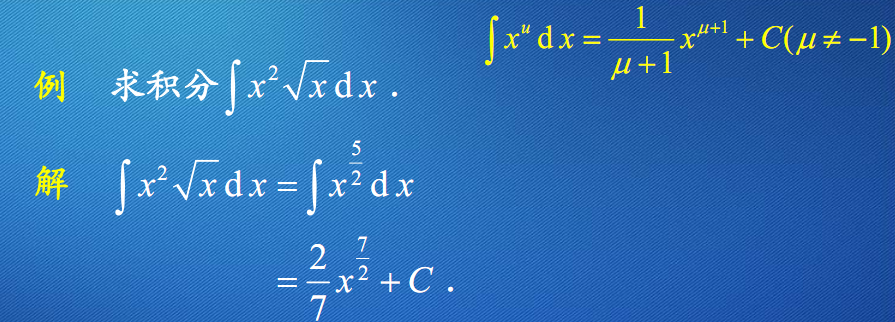
例4

例5

例6

例7
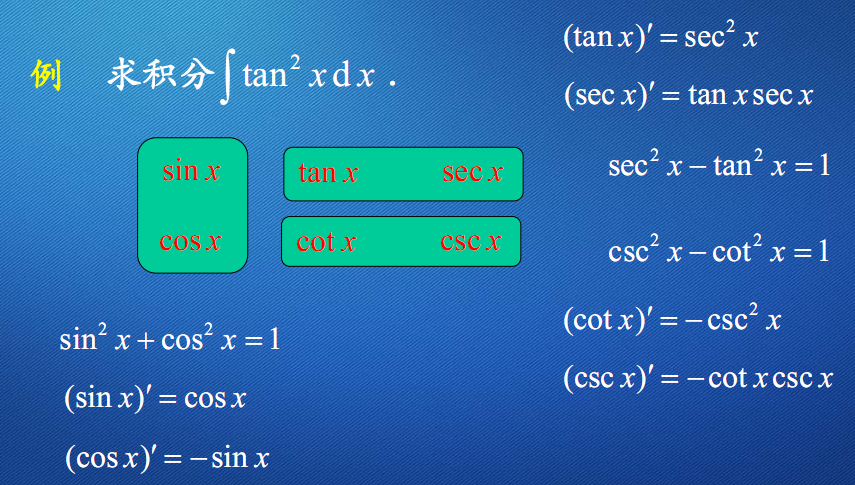
例8
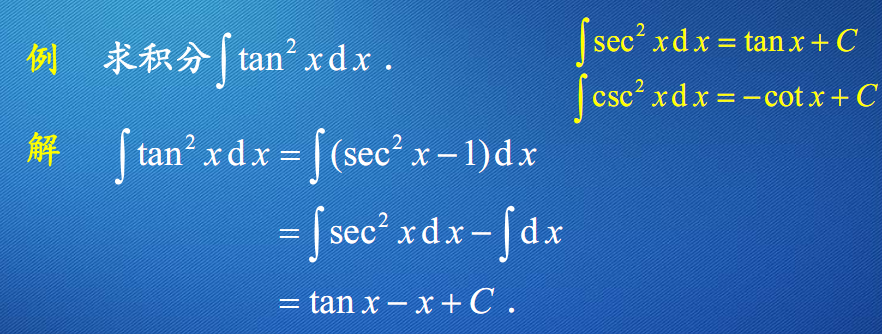
例9

例10

例11
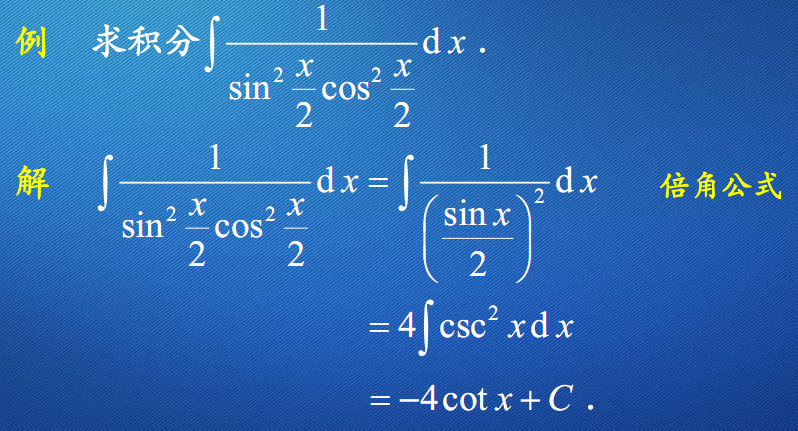
例12

例13
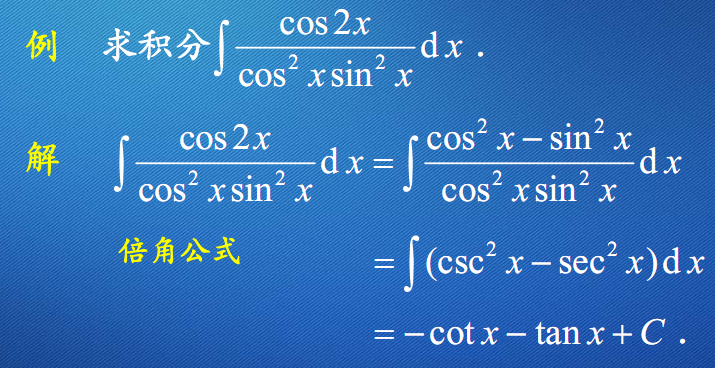
本文链接: 4-2不定积分的性质与基本积分表

