- 无穷小比较的定义
- 等价无穷小的性质
无穷小比较的定义
引出

两个无穷小的比较 定义





$x \to 0$时,$\sqrt[n]{1+x}-1 \sim \dfrac{1}{n}x$
等价无穷小的性质
定理

等价无穷小替换定理
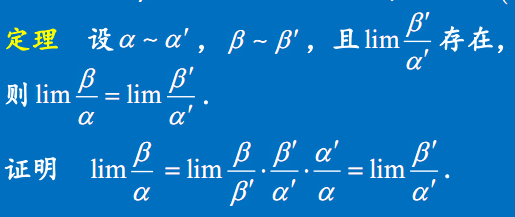
例题
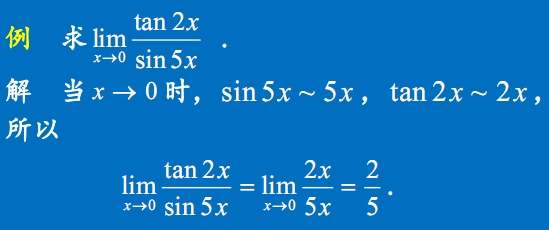
$x \to 0$时$tanx \sim x,sinx \sim x$
$x \to 0$时,$1-cosx \sim \dfrac{1}{2}x^2$,$arctanx \sim x$,$arctanx^2 \sim x^2$.

只有相乘或相除的因式才能用等价无穷小代替

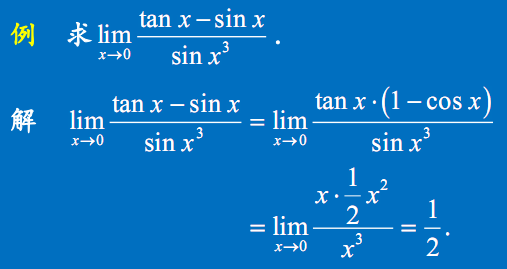
- $tanx=\dfrac{sinx}{cosx}$
- $sinx=tanx\times cosx$
习题
习题1

$$
\begin{align}
\lim \limits_{x \to 0}\dfrac{\sqrt{1+xsinx}-cos2x}{xtanx}&= \nonumber \\
\lim \limits_{x \to 0}\dfrac{\sqrt{1+xsinx}-1+(1-cos2x)}{xtanx}&= \nonumber \\
\lim \limits_{x \to 0}(\dfrac{\dfrac{1}{2}xsinx}{xtanx}+\dfrac{1-cos2x}{xtanx})&= \nonumber \\
\end{align}
$$
$\lim \limits_{x \to 0}\dfrac{\dfrac{1}{2}xsinx}{xtanx}=
\lim \limits_{x \to 0}\dfrac{\dfrac{1}{2}x^2}{x^2}=
\dfrac{1}{2}$
$\lim \limits_{x \to 0}\dfrac{1-cos2x}{xtanx}=\dfrac{\dfrac{1}{2}(2x)^2}{x^2}=2$
所以,$原式=\dfrac{1}{2}+2=\dfrac{5}{2}$
- $1-cosx \sim \dfrac{1}{2}x^2$
- $\sqrt[n]{1+x}-1 \sim \dfrac{1}{n}x$
习题2

$\lim \limits_{x \to 0}\dfrac{sinx(1-cosx)}{x^3}=\dfrac{x\times \dfrac{1}{2}x^2}{x^3}=\dfrac{\dfrac{1}{2}}{1}=\dfrac{1}{2}$,所以是同阶无穷小,等价无穷小极限为1,高阶无穷小极限为0(分子趋近与0的速度(阶数)大),低阶无穷小极限为无穷大,分母趋近于0的速度大(阶数大),则分子阶数小。
习题3

$\lim \limits_{x \to 0}\dfrac{1-cosx}{xsinx}=\dfrac{\dfrac{1}{2}x^2}{x^2}=\dfrac{1}{2}$
习题4

- 有限个无穷小的和式无穷小,\left|\beta(x)\right|是无穷小,\left|\alpha(x)\right|是无穷小,所以两者之和也是无穷小,排除A
- 有限个无穷小的乘积是无穷小,$\alpha^2(x)$,$\beta^2(x)$也是无穷小,两者的和也是无穷小。排除B
- $\lim \limits_{x \to x_0}ln[1+\alpha(x)\beta(x)]=0 $也是无穷小,排除C
- 由两个无穷小之间的关系 定理可以知道,两个无穷小的商的结果又多种可能,可能是0(高级无穷小),可能是1(等价无穷小),可能是$\infty$(低阶),可能是一个常数C(同阶无穷小),所以结果不一定是无穷小(极限为0)
习题5

解:令$t=x-1=1-1=0$则$x=1+t$,当$x \to 1$时$t \to 0$,则:
$
\lim \limits_{x \to 1}\dfrac{\dfrac{1-x}{1+2x}}{\sqrt{x}-1}
=\lim \limits_{t \to 0}\dfrac{\dfrac{1-(1+t)}{1+2(1+t)}}{\sqrt{1+t}-1}\\
=\lim \limits_{t \to 0}\dfrac{\dfrac{t}{3+2t}}{\dfrac{1}{2}t}
=\lim \limits_{t \to 0}\dfrac{\dfrac{1}{3+2t}}{\dfrac{1}{2}}
=\lim \limits_{t \to 0}\dfrac{2}{3+2t}
=\dfrac{2}{3}
$
所以是同阶无穷小,非等价无穷小
无穷小公式汇总
$x \to 0$是有:
- $sinx \sim x$
- $tanx \sim x$
- $arctanx \sim x$
- $\sqrt[n]{1+x}-1 \sim \dfrac{1}{n}x$
- $1-cosx \sim \dfrac{1}{2}x^2$
本文链接: 1-7无穷小的比较

