一阶系统
用一阶微分方程描述其动态过程的系统称为一阶系统。
微分方程:
$T\dfrac{dc(t)}{dt}+c(t)=r(t)$
传递函数
$\dfrac{C(s)}{R(s)}=\dfrac{1}{Ts+1}$
一阶系统例子
RC电路,输出$u_c(t)$和输入$u_r(t)$之间的关系:
典型闭环控制一阶系统是一个惯性环节

典型输入信号作用下一阶系统的相应过程
在以下的分析和计算中均假定系统的初始工作条件为$0$
一阶系统的单位阶跃响应

$C(s)=\varPhi(s)R(s)=\dfrac{1}{Ts+1}\cdot\dfrac{1}{s}=\dfrac{1}{s}-\dfrac{1}{s+\dfrac{1}{T}}$
两端取拉式反变换得到一阶系统单位阶跃响应:
$$
c(t)=1-e^{-\dfrac{t}{T}}
$$
单位阶跃响应曲线
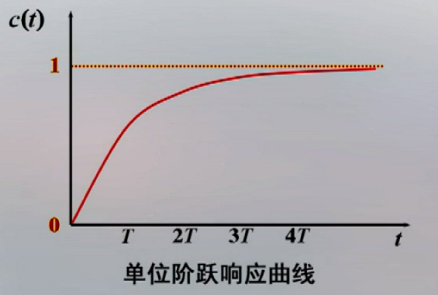
一阶系统单位阶跃响应的两个重要特点
1.可以用时间常数$T$来度量系统输出量的值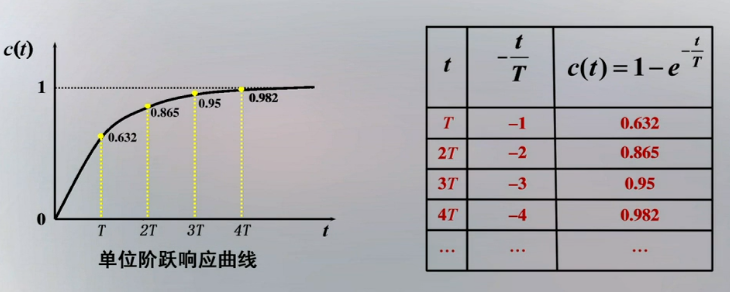
2.响应曲线的斜率可以通过对$t$求导得到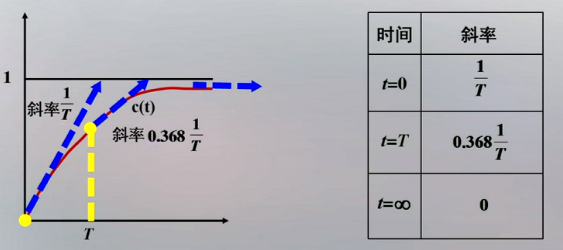
系统运动的最大变化率刚好是初始斜率,即$\dfrac{1}{T}$

