主要内容
- 函数的概念
- 函数的特性
- 初等函数
函数的概念
函数定义


构成函数的要素
- 定义域$D_f$
- 对应法则$f$
如果两者一样则是同一个函数
函数的定义域
- 根据问题的实际背景确定的

- 另一种是抽象地
用算式表达的函数,这时我们约定:函数的定义域就是使表达式有意义的一切实数所组成的集合,这种定义域称作是函数的自然定义域

函数的图形

常见函数
常数函数

绝对值函数
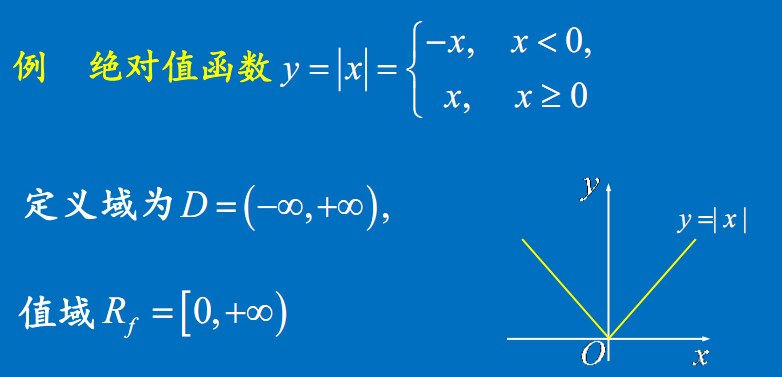
符号函数

取整函数

分段函数
这种自变量在不同变化范围中,对应法则用不同的式子来表示的函数称为分段函数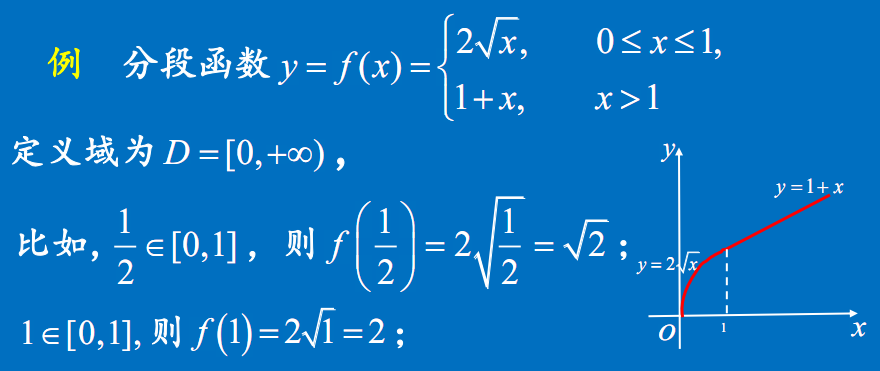
函数的特性
- 函数的有界性
- 函数的单调性
- 函数的奇偶性
- 函数的周期性
函数的有界性
上界

下界

有界

无界
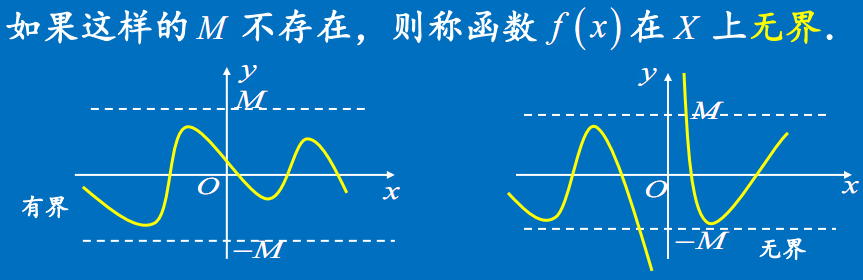
实例

函数的单调性
单调增加

单调减少

单调增加或单调减少的函数统称为单调函数
实例

函数的奇偶性
奇函数定义

偶函数定义
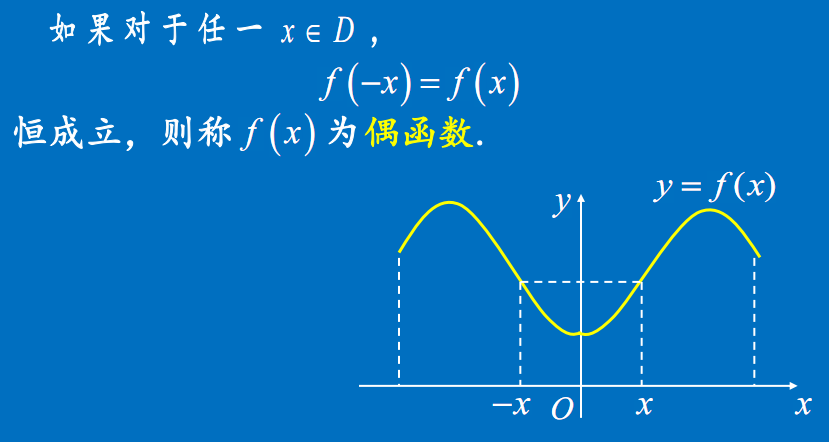
实例

函数的周期性

注意
- 1.通常我们说的周期函数的周期是指
最小正周期比如,函数$sinx$,$cosx$都是以$2π$为周期(最小正周期)的周期函数,函数$tanx$是以为$π$周期(最小正周期)的周期函数 - 2.并非所有函数都有最小正周期
狄利克雷函数没有最小正周期

初等函数
基本初等函数


对数函数
对数函数性质
$log_aM^n=nlog_aM$
$log_{a^n}M=\dfrac{1}{n}log_aM$
除法公式
${log_a}{\dfrac{M}{N}}=log_aM-log_aN$
乘法公式
${log_a}{MN}=log_aM+log_aN$
换底公式
$log_ba=\dfrac{log_ca}{log_cb}$
倒数公式
$\dfrac{1}{log_ab}=log_ba$
对数函数图像
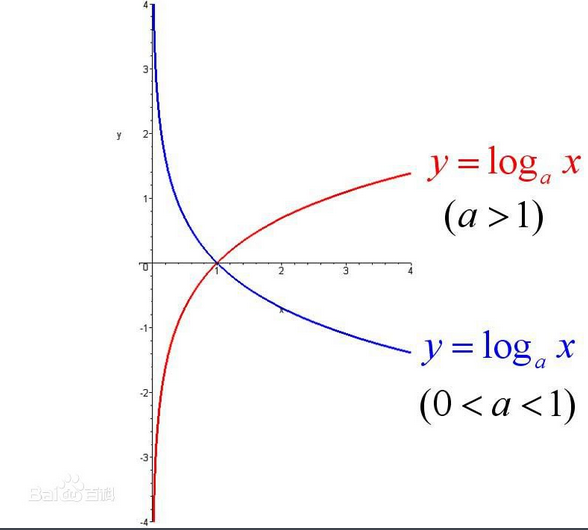
初等函数
定义
由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成的,并可用一个式子表示的函数,称为初等函数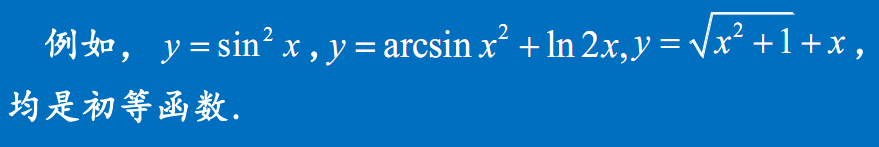
习题





解:狄利克雷函数不是初等函数,它不能由基本初等函数经过有限步加减乘除复合运算得到。
本文链接: 第一讲 函数与初等函数

