第1章
和的概率
$$
\begin{aligned}
P(A\bigcup B)=&P(A)+P(B)-P(AB) \\
=&P(A)+P(\overline{A}B) \\
\end{aligned}
$$
$$P(A\bigcup\overline{B})=1-P(\overline{A}B)$$
$A(A\bigcup B)=A\bigcap (A\bigcup B)=A$
条件概率

$P(B|A)=\dfrac{P(AB)}{P(A)}$
乘法公式

注意:(1)独立事件的条件概率与条件无关,
(2)独立事件计算概率尽可能表示为乘积事件
全概率公式


第2章
常见离散型分布律
0-1分布
$X \sim 0-1(p),X \sim B(1,p)$
分布律
$P(X=K)=p^k(1-p)^{1-k},k=0,1$
二项分布
$X \sim B(n,p)$
分布律
$P{X=k}=C^k_np^k(1-p)^{n-k},k=0,1,…,n$
泊松分布
$X \sim P(\lambda)$,或者$X \sim \pi(\lambda)$
分布律
$P{X=k}=\dfrac{\lambda^ke^{-\lambda}}{k!},k=0,1,2,…$
几何分布
$X \sim G(p)$
分布律
$P(X=k)=p(1-p)^{k-1},k=1,2,3,…$
分布函数
定义
$F(x)=P(X\le x)$
分布函数的几何意义
小于等于$x$的所有概率的和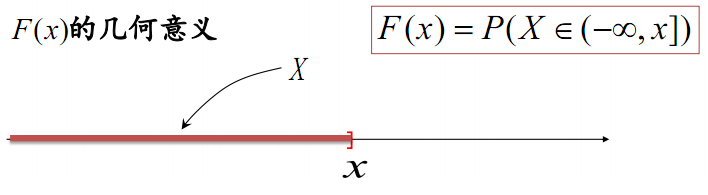
连续型随机变量的分布
性质
一下的几种分布都满足如下性质:
$f(x)\ge 0$
$\int^{+\infty}_{-\infty}f(x)dx=1$
均匀分布
符号
$X \sim U(a,b)$
概率密度函数
$$
f(x)=\begin{cases}
\dfrac{1}{b-a}&,a<x<b, \\
0&,其他
\end{cases}
$$
分布函数
$$
F(x)=\int^{x}_{-\infty}f(x)dx=\begin{cases}
0,&x\le a, \\
\dfrac{x-a}{b-a}&,a<x<b, \\
1,&x\ge b
\end{cases}
$$
指数分布
符号
$X\sim E(\lambda)$
概率密度函数
$$
f(x)=\begin{cases}
\lambda e^{-\lambda x} &,x>0, \\
0 &,x\le 0
\end{cases}
$$
分布函数
$$
F(x)=\int^{x}_{-\infty}f(x)dx=\begin{cases}
1-e^{-\lambda x} &,x<0 \\
0 &,x\le 0
\end{cases}
$$
指数分布具有无记忆性
正态分布
符号
$X\sim N(\mu,\sigma)$
$\mu,\sigma(\sigma>0)$为常数,正态分布也叫高斯分布
概率密度函数
$$
f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{(x-\mu)^2}{2\sigma^2}},-\infty<x<+\infty
$$
分布函数
$$
F(x)=\dfrac{1}{\sqrt{2\pi}\sigma}\int^{x}_{-\infty}e^{-\dfrac{(x-\mu)^2}{2\sigma^2}}dx,-\infty<x<+\infty
$$
特有性质
$f(x)$的图形关于$x=\mu$对称
$x=\mu$时,$f(x)$取得最大值,$f(\mu)=\dfrac{1}{\sqrt{2\pi}\sigma}$
在$x=\mu+\sigma$处有拐点.
概率密度函数$f(x)$以$x$轴为渐近线
第4章 随机变量的数字特征
随机变量的数学期望
离散型随机变量的数学期望
$E(X)=\sum\limits_{k=0}^{\infty}x_kp_k$
连续型随机变量的数学期望
$$
E(X)=\int^{+\infty}_{-\infty}xf(x)dx
$$
随机变量函数的数学期望
离散型随机变量
$E(Y)=E(g(X))=\sum\limits_{k=0}^{\infty}g(x_k)p_k$
连续型随机变量
$E(Y)=E(g(X))=\int^{+\infty}_{-\infty}g(x)f(x)dx$
数学期望的性质
性质1
若$C$是常数,则:$E(C)=C$
性质2
$C$是常数,$X$是随机变量,则:$E(CX)=CE(X)$
性质3
若$X$,$Y$是两个随机变量,则:$E(X+Y)=E(X)+E(Y)$,
$E(k_1X_1+k_2X_2+\cdots+k_nX_n+C)=k_1E(X_1)+k_2E(X_2)+\cdots+k_nE(X_n)+C$
性质4
若$X$,$Y$为两个相互独立的随机变量,则:$E(XY)=E(X)E(Y)$
随机变量的方差
方差
$D(X)=E([X-E(X)]^2)=E(X^2)-[E(x)]^2$,
方差等于平方的期望减去期望的平方
随机变量$X$的方差反应了$X$的取值与其数学期望的偏离程度。若D(X)较小,则X的取值比较集中,否则,X的取值就比较分散.
方差D(X)是刻画X取值分散程度的一个量.
标准差 均方差
$\sqrt{D(X)}$
方差的性质
性质1
若$C$是常数,则$D(C)=0$
性质2
设$C$为常数,$X$为随机变量.$D(CX)=C^2D(X)$,从方差之中提出常数,常数要平方.
性质3
设$X$,$Y$为两个互相独立的随机变量,则有:
$D(X+Y)=D(X)+D(Y)$
性质4
$D(X)=0$的充分必要条件是$X$以概率$1$取常数$C$,即$P(X=C)=1$,此时$C=E(X)$
几种重要的分布的数学期望及方差
0-1分布
$P(X=0)=1-p,P(X=1)=p,(0<p<1).$
$E(X)=p$,$D(X)=p(1-p)$
二项分布
$P(X=k)=C^k_np^k(1-p)^{n-k},k=0,1,\cdots,n.$
$E(X)=np$,$D(X)=np(1-p)$
泊松分布
$P(X=k)=\dfrac{\lambda^ke^{-\lambda}}{k!},k=0,1,\cdots.$
$E(X)=\lambda$,$D(X)=\lambda$.
均匀分布
$$
f(x)=\begin{cases}
\dfrac{1}{b-a} &,a<x<b, \\
0 &,其他
\end{cases}
$$
$E(X)=\dfrac{a+b}{2}$,$D(X)=\dfrac{(b-a)^2}{12}$
指数分布
$$
f(x)=\begin{cases}
\lambda e^{-\lambda} &,x>0, \\
0 &,x\le 0.
\end{cases}
$$
$E(X)=\dfrac{1}{\lambda}$,$D(X)=\dfrac{1}{\lambda^2}$.
正态分布
$f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}e^{-\dfrac{(x-\mu)^2}{2\sigma^2}},-\infty<x<+\infty$.
$E(X)=\mu$,$D(X)=\sigma^2$
原文链接: 概率论公式集合

