- 引例
- 导数的定义
- 导数的几何意义
- 函数可导性与连续性的关系
引例
变速直线运动的速度



切线问题

切线定义

切线的斜率

规律
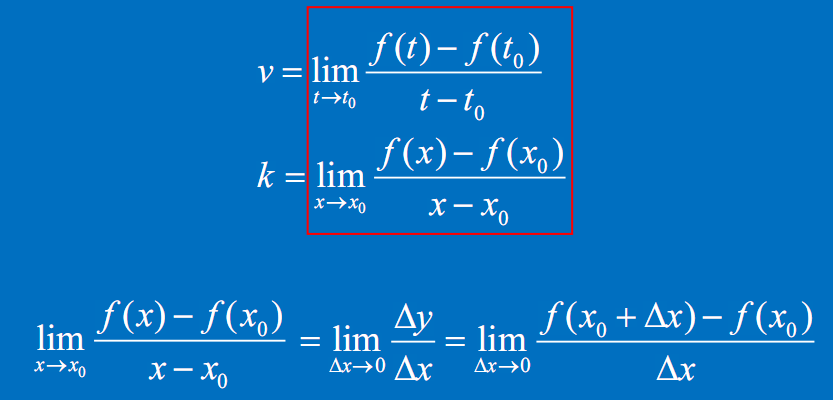
导数的定义
函数在一点处的导数

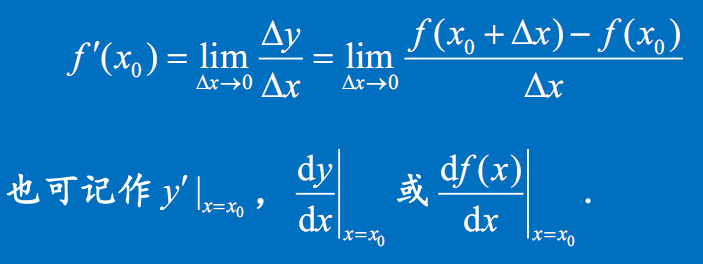

不可导

导函数的定义



求导数举例
例1 常数的导数为零

$(C)’=0$
例2 幂函数的导数

$(x^u)’=ux^{u-1}$
常见幂函数的导数

- $x’=1$
- $(x^2)’=2x$
- $(\sqrt{x})’=\dfrac{1}{2\sqrt{x}}$
- $(\dfrac{1}{x})’=-\dfrac{1}{x^2}$
例3 指数函数的导数

$(a^x)’=a^x\ln a$,若$a=e$,则$(e^x)’=e^x$
例4 对数函数的导数

$(\log_ax)’=\dfrac{1}{x\cdot\ln a}$,若$a=e^x$,则,$(\ln x)’=\dfrac{1}{x}$
例5 正弦函数 余弦函数的导数

$(\sin x)’=\cos x$
$(\cos x)’=-\sin x$
例7 绝对值函数在x=0不可导

单侧导数

左导数与右导数统称为单侧导数
导数存在定理: 左右导数存在且相等
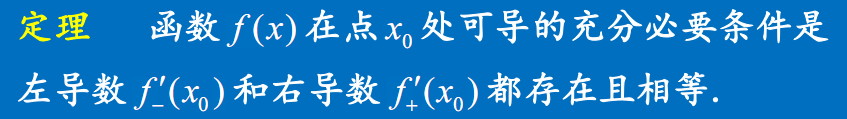
函数在闭区间内可导定义

导数的几何意或
切线 切线方程
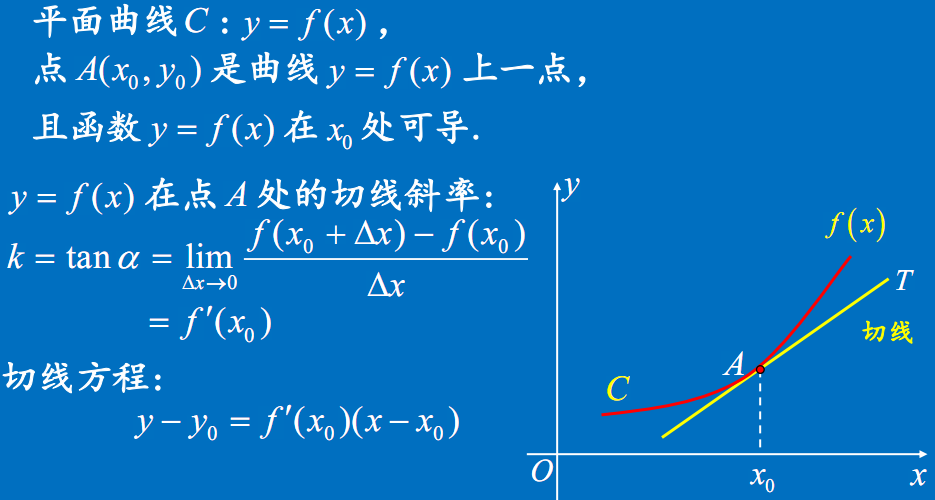
法线 法线方程

导数为无穷大的切线为x轴

例子 求切线方程 法线方程

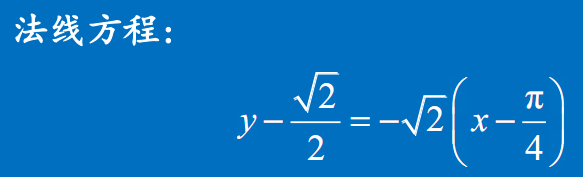
函数可导性与连续性的关系
可导必连续

连续不一定可导


小结
函数在一点处的导数
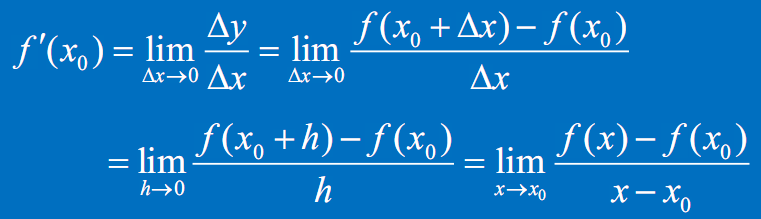
导数公式
- $(C)’=0$
- $(x^u)’=ux^{u-1}$
- $x’=1$
- $(x^2)’=2x$
- $(\sqrt{x})’=\dfrac{1}{2\sqrt{x}}$
- $(\dfrac{1}{x})’=-\dfrac{1}{x^2}$
- $(a^x)’=a^x\ln a$,若$a=e$,则$(e^x)’=e^x$
- $(\log_ax)’=\dfrac{1}{x\cdot\ln a}$,若$a=e^x$,则,$(\ln x)’=\dfrac{1}{x}$
- $(\sin x)’=\cos x$
- $(\cos x)’=-\sin x$
习题
题1

这题考导数定义的形式:
$$
\begin{align}
f’(x_0)=&\lim \limits_{\Delta x \to x_0 }\dfrac{\Delta y}{\Delta x} \nonumber \\
=&\lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \nonumber \\
=&\lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+h)-f(x_0)}{h} \nonumber \\
=&\lim \limits_{x \to x_0 }\dfrac{f(x)-f(x_0)}{x-x_0} \nonumber \\
\end{align}
$$
解:这题神似第三中形式:
$$
\begin{aligned}
&\lim \limits_{x \to 1 }\dfrac{f^2(x)-1}{x^2-1} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(f(x)-1)(f(x)+1)}{(x-1)(x+1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(f(x)-1)}{(x-1)}\dfrac{(f(x)+1)}{(x+1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(f(x)-1)}{(x-1)}\lim \limits_{x \to 1 }\dfrac{(f(x)+1)}{(x+1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(f(x)-1)}{(x-1)} \dfrac{(1+1)}{(1+1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(f(x)-1)}{(x-1)} \nonumber \\
=&f’(1) \nonumber \\
=&2 \nonumber \\
\end{aligned}
$$
题2 导数的定义变型

这题考的是导数定义的几种变型:
$$
\begin{align}
f’(x_0)=&\lim \limits_{\Delta x \to x_0 }\dfrac{\Delta y}{\Delta x} \nonumber \\
=&\lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \nonumber \\
=&\lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+h)-f(x_0)}{h} \nonumber \\
=&\lim \limits_{x \to x_0 }\dfrac{f(x)-f(x_0)}{x-x_0} \nonumber \\
\end{align}
$$
这题跟第一种形式神似,我们要配出第一中形式的样子来就可以了。
$$
\begin{aligned}
& f’(x_0) \nonumber \\
=&\lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \nonumber \\
=&\lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+3\Delta x)-f(x_0)}{3\Delta x} \nonumber \\
=&\dfrac{1}{3} \lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+3\Delta x)-f(x_0)}{\Delta x} \nonumber \\
\end{aligned}
$$
所以,$ \lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+3\Delta x)-f(x_0)}{\Delta x}=3f’(x_0) $
解:这题考导数定义
题3 求导

解:指数函数导数公式:$(x^u)’=ux^{u-1}$
所以$y’=(\dfrac{1}{x^3})’=(x^{-3})’=-3u^{-3-1}=-3u^{-4}=- \dfrac{3}{u^4}$
题4 求切线斜率
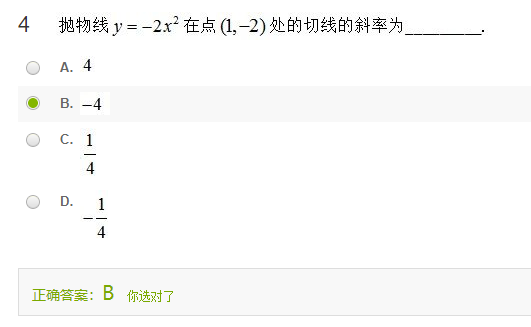
解:
斜率$k=y’=(-2x^2)’=-4x$,所以在点$(1,-2)$处$k=-4\times 1=-4$
题5

这题考导数定义的形式:
$$
\begin{align}
f’(x_0)=&\lim \limits_{\Delta x \to x_0 }\dfrac{\Delta y}{\Delta x} \nonumber \\
=&\lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+\Delta x)-f(x_0)}{\Delta x} \nonumber \\
=&\lim \limits_{\Delta x \to x_0 }\dfrac{f(x_0+h)-f(x_0)}{h} \nonumber \\
=&\lim \limits_{x \to x_0 }\dfrac{f(x)-f(x_0)}{x-x_0} \nonumber \\
\end{align}
$$
这里使用第三个导数定义是,把$x_0=0,f(x_0)=f(0)=0$代入得:
$$
\begin{aligned}
f’(0)=&\lim \limits_{x \to 0 }\dfrac{f(x)-f(0)}{x-0} \nonumber \\
=&\lim \limits_{x \to 0 }\dfrac{f(x)}{x} \nonumber \\
=&\lim \limits_{x \to 0 }\dfrac{\dfrac{x}{1-e^{\frac{1}{x}}}}{x} \nonumber \\
=&\lim \limits_{x \to 0 }\dfrac{\dfrac{1}{1-e^{\frac{1}{x}}}}{1} \nonumber \\
=&\lim \limits_{x \to 0 }\dfrac{1}{1-e^{\frac{1}{x}}} \nonumber \\
\end{aligned}
$$
所以最终得到:$f’(0)=\lim \limits_{x \to 0 }\dfrac{1}{1-e^{\frac{1}{x}}}$,如果这个极限存在则导数存在,
$\lim \limits_{x \to 0^+ }\dfrac{1}{x}=+\infty$
$\lim \limits_{x \to 0^- }\dfrac{1}{x}=-\infty$
$\lim \limits_{x \to 0^+ }\dfrac{1}{1-e^{\frac{1}{x}}}=\dfrac{1}{1-(+\infty)}=0$
$\lim \limits_{x \to 0^- }\dfrac{1}{1-e^{\frac{1}{x}}}=\dfrac{1}{1-0}=1$
左右极限不相等,所以极限不存在,所以在这点的导数不存在。
本文链接: 2-1导数概念

