1-8函数的连续性与间断点

发表于 | 更新于 | 分类于 ， ， ，

 

  • 函数的连续性
  • 函数的间断点

西数的连续性

增量

连续


连续定义


左连续右连续


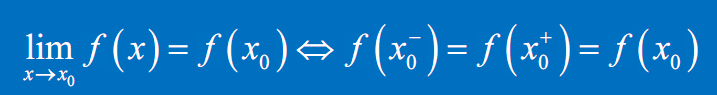
函数在该区间上连续

在区间上每一点都连续的函数,叫做在该区间上的连续函数,或者说函数在该区间上连续
如果区间包含端点,那么函数在右端点连续是指左连续,在左端点连续是指右连续

函数的间断点

间断点(不连续)的三种情况

间断点类型


例题

可去间断点


等价无穷小：$x \to 0$时$sinx \sim x$

跳跃间断点

无穷间断点

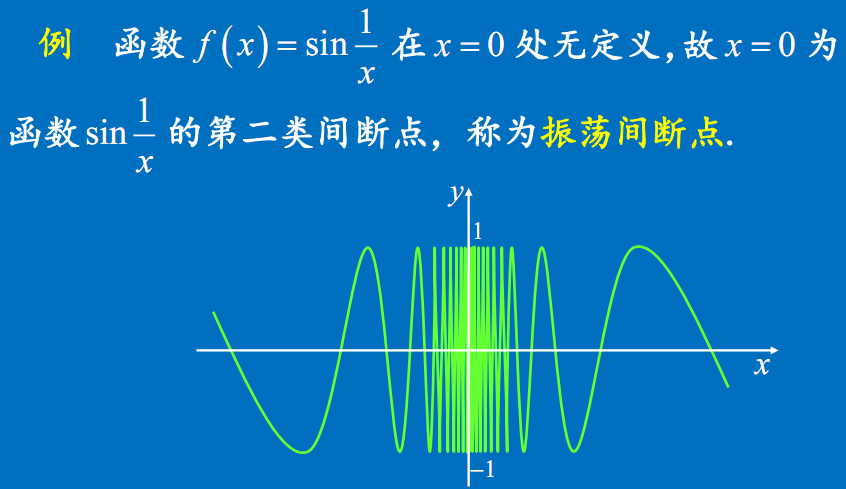
震荡间断点

习题

习题1


$f(0^-)=0-1=-1$,$f(0^+)=0+1=1$,所以是跳跃间断点

习题2


$x \to 0^+$时，$\dfrac{1}{x} \to +\infty$,$\dfrac{-1}{x} \to -\infty$,$\lim e^{\dfrac{-1}{x}} =\lim e^{-\infty }=0$,
所以$\lim \limits_{x \to 0^+}1-e^{\dfrac{-1}{x}}=1-0=1=f(0)=1$,所以右连续，
$x \to 0^-$时， $\dfrac{1}{x} \to -\infty$，则$\dfrac{-1}{x} \to +\infty$，则$\lim e^{\dfrac{-1}{x}} =\lim e^{+\infty }=+\infty$，
所以$\lim \limits_{x \to 0^+}1-e^{\dfrac{-1}{x}}=1-(+\infty) = -\infty \ne f(0)=1$,所以左不连续。
所以不连续

习题3


假设函数$f(x)$在点x的某去心邻域内有定义,如果函数$f(x)$有下列三种情形之一:
(1)在$x=x_0$处没有定义;
(2)虽然在$x=x_0$处有定义,但$\lim \limits_{x \to x_0}f(x)$不存在;
(3)虽然在$x=x_0$处有定义$\lim \limits_{x \to x_0}f(x)$存在但$\lim \limits_{x \to x_0}f(x)\ne f(x)$;
则称函数$f(x)$在点$x_0$时不连续;点$x_0$称为$f(x)$的不连续点,或间断点

选项D中，函数在x=0处没有定义，所以函数$f(x)$在点$x=0$不连续.

例题4


由连续的定义可以以看出，极限存在，并且极限等于函数值则连续，单凭极限存在并不能退出联系，所以不满足必要条件，而连续则可以推出极限存在，并且极限值等于函数值。满足充分条件。不是必要条件，更不是充要条件。

例题5


连续说明 极限值等于函数值a，所以求出极限值即可得出a的值，
$$
\begin{align}
&\lim \limits_{x \to -1}\dfrac{x^2-2x-3}{x+1} \nonumber \\
=& \lim \limits_{x \to -1}\dfrac{(x+1)(x-3)}{x+1} \nonumber \\
=& \lim \limits_{x \to -1}x-3 \nonumber \\
=& -4 \nonumber \\
\end{align}
$$
所以$a=-4$

本文链接: 1-8函数的连续性与间断点

0%