自动控制原理MOOC作业2
第2题
课后习题2-22
试用梅森增益公式求出如图所示系统的传递函数$C(s)/R$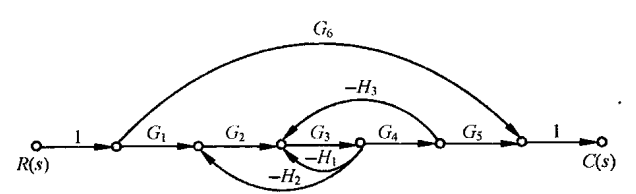
草稿
标出节点如下图所示: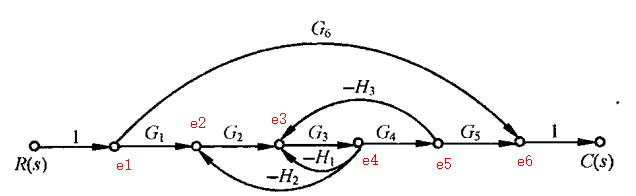
单独回路
| 单独回路 | 回路增益 |
|---|---|
| $e_2\to e_3\to e_4\to e_2$ | $L_1=-G_2G_3H_2$ |
| $e_3\to e_4\to e_3$ | $L_2=-G_3H_1$ |
| $e_3\to e_4\to e_5\to e_3$ | $L_3=-G_3G_4H_3$ |
互不接触回路
因为回路$L_1,L_2,L_3$都含有公共的节点$e_3$,所以没有互不接触的回路。
流图特征式
$$
\begin{aligned}
\Delta=&1-\sum L_a \\
=&1-(L_1+L_2+L_3) \\
=&1+G_3H_1+G_2G_3H_2+G_3G_4H_3 \\
\end{aligned}
$$
前向通路
$R(s)\to e_1\to e_2\to e_3\to e_4\to e_5\to e_6\to G(s)$,
- 前向通路增益$p_1=G_1G_2G_3G_4G_5$,
- 该前向通路与所以的单独回路都接触(因为都有节点$e_3$)所以余子式:
$$
\require{cancel}
\begin{aligned}
\Delta_1=&\Delta-\text{包含接触的单独回路增益的所有乘积项} \\
=&1-(\bcancel{L_1}+\bcancel{L_2}+\bcancel{L_3}) \\
=&1 \\
\end{aligned}
$$
$R(s)\to e_1\to e_6\to C(s)$,
- 前向通路增益$p_2=G_6$
- 因为该前向通路没有与任何单独回路接触,所以余子式:
$\Delta_2=\Delta=1+G_3H_1+G_2G_3H_2+G_3G_4H_3$
传递函数
$$
\begin{aligned}
\dfrac{C(s)}{R(s)}=&\dfrac{1}{\Delta}(p_1\Delta_1+p_2\Delta_2) \\
=&\dfrac{1}{\Delta}(p_1\Delta_1+p_2\Delta) \\
=&\dfrac{1}{\Delta}p_1\times 1+p_2 \\
=&\dfrac{p_1}{\Delta}+p_2 \\
=&\dfrac{G_1G_2G_3G_4G_5}{1+G_3H_1+G_2G_3H_2+G_3G_4H_3}+G_6 \\
\end{aligned}
$$
解
单独回路
$L_1=-G_2G_3H_2$
$L_2=-G_3H_1$
$L_3=-G_3G_4H_3$
流图特征式
$$
\begin{aligned} \Delta=&1-\sum L_a \\ =&1-(L_1+L_2+L_3) \\ =&1+G_3H_1+G_2G_3H_2+G_3G_4H_3 \\ \end{aligned}
$$
前向通路
$p_1=G_1G_2G_3G_4G_5$,$\Delta_1=1$
$p_2=G_6$,$\Delta_2=\Delta$
传递函数
$$
\begin{aligned} \dfrac{C(s)}{R(s)}=&\dfrac{1}{\Delta}(p_1\Delta_1+p_2\Delta_2) \\
=&\dfrac{G_1G_2G_3G_4G_5}{1+G_3H_1+G_2G_3H_2+G_3G_4H_3}+G_6 \\ \end{aligned}
$$
原文链接: null

