数列的极限
数列是个特殊的函数
数列极限是我们极限思想的起源
数列极限是相对简单的而且直观的
本文内容
- 数列的定义
- 数列极限的定义
- 收敛数列的性质
数列的定义

数列实例
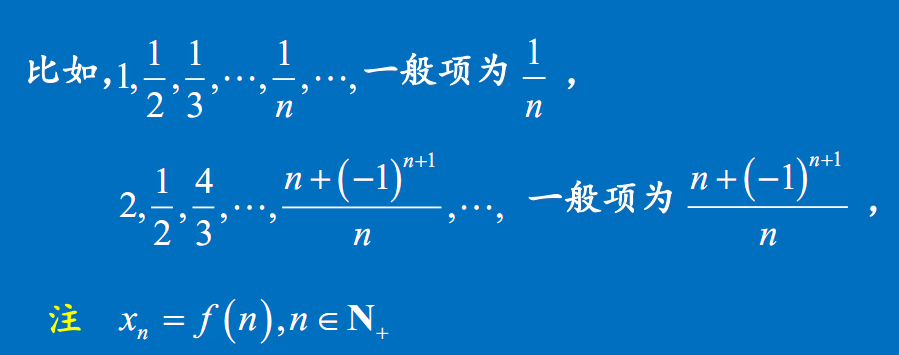
数列极限的定义
引出
我国古代数学家刘徽利用圆内接正多边形来推算圆面积的方法—-割圆术
先做内接正六多边形,记该内接正6多边形面积为$A_1$: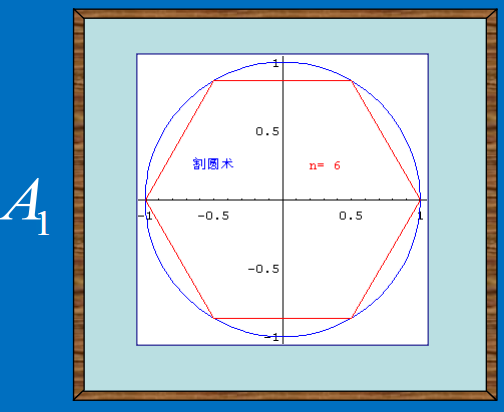
然后做内接正12多边型,记该内接正12多边型的面积为$A_2$: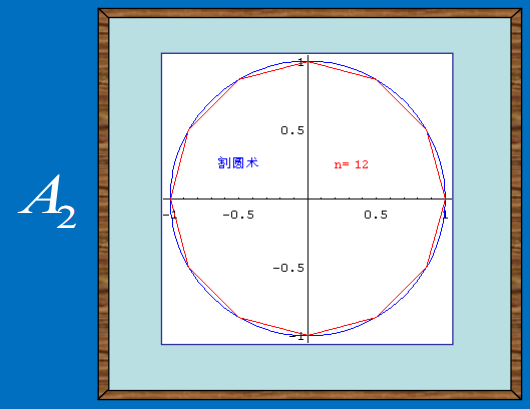
然后做内接正24多边型,记该内接正24多边型的面积为$A_3$: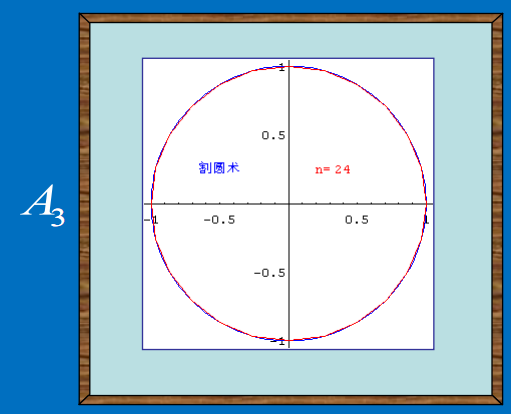
……
一直这样下去,得到正n多边形的面积$A_n$,当n越大,$A_n$就越接近圆的面积。
当$n\rightarrow \gt \infty$ 时,${A_n}$也无限接近于某一确定的数值,这个数值称为数列${A_n}$当时$n\rightarrow \gt \infty$的极限
例子

可以通过两个数的差的绝对值来判断他们的接近程度,差越接近于0,两个数则越接近。$x_n$与$1$的差的绝对值如下: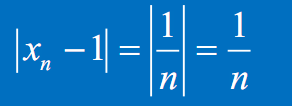
可以看出两者的绝对值只差$\dfrac{1}{n}$决定了$x_n$与$1$的接近程度。如果认为两者差的绝对值小于$\dfrac{1}{100}$就可以的话,则可以求出n如下:


$\dfrac{1}{100}$,$\dfrac{1}{10000}$,$\dfrac{1}{1000000}$,$\cdot$这样表述太麻烦了,现在用字母$\varepsilon$来表示这些任意给定的小的正数。把上面的过程简化如下:

数列极限定义



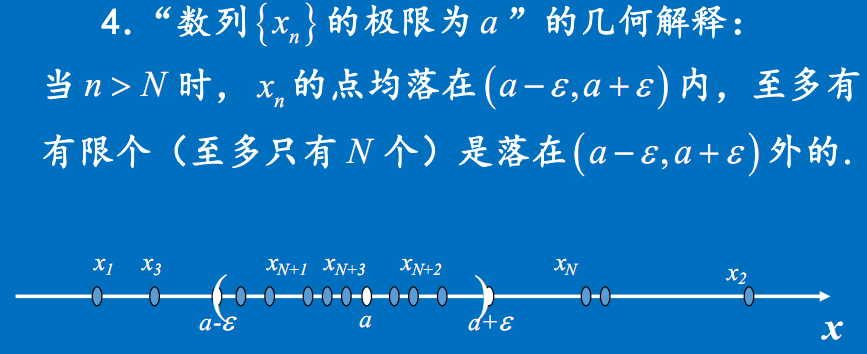
数列极限几何意义
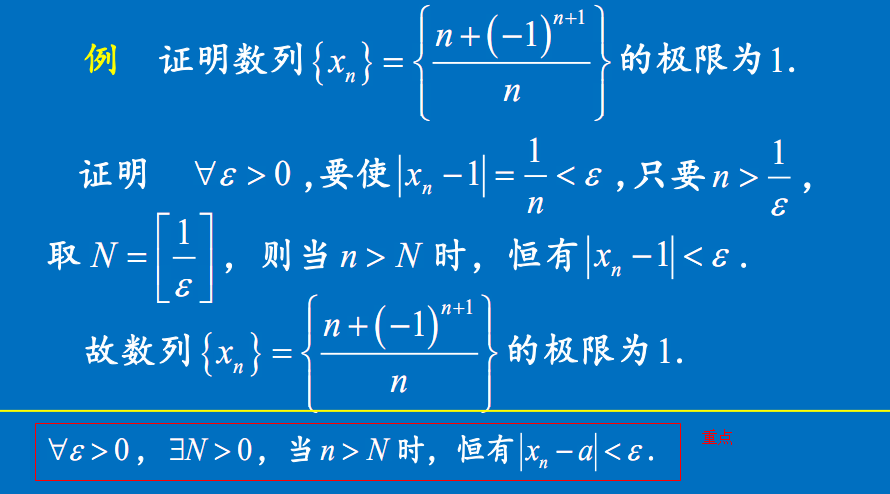
利用定义证明极限
关键点:
- 数列通项减去极限值$\lt \varepsilon$
- 求出n>$\varepsilon$的表达式
- 令N=上述$\varepsilon$的表达式
- 则当$n>N$时,恒有数列通项减去极限值$\lt \varepsilon$成立,所以得证。
证明 等比数列极限为0

收敛数列的性质
定理1 极限的唯一性
如果数列${x_n}$收敛,那么它的极限唯一的。
有界性定义


定理2 收敛数列的有界性
定理2(收敛数列的有界性)如果数列${x_n}$收敛,则数列${x_n}$一定有界
推论:如果数列无界,则其一定发散;
定理3 收敛数列的保号性

子数列定义

定理4 收敛数列与其子数列间的关系

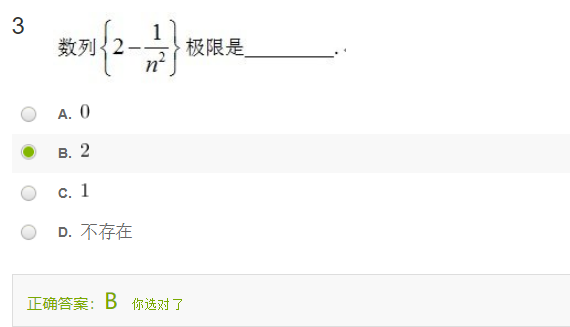
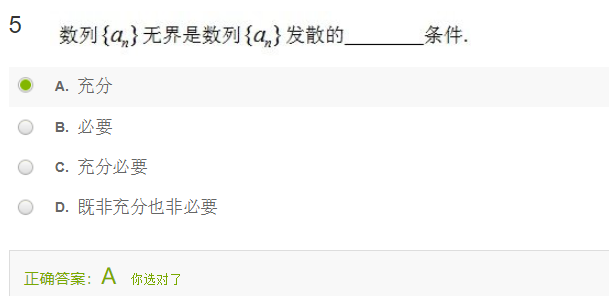
习题


定理四:
- 如果数列${x_n}$收敛于a,则它的任一子数列也收敛,且其极限也为a
- 推论若数列${x_n}$的某个子列发散或某两个子列收敛于两个不同的极眼,则该数列${x_n}$必发散
本文链接: 第一讲 数列及其极限

