自动控制原理 作业题 2-17
2-17已知控制系统结构图如图2-56所示,试通过结构图等效变换求系统传递函数$C(s)/R(s)$。
图a
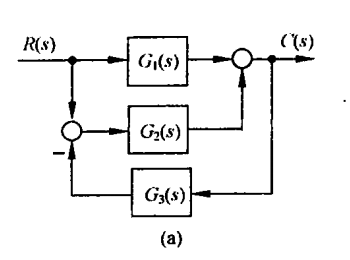
图b
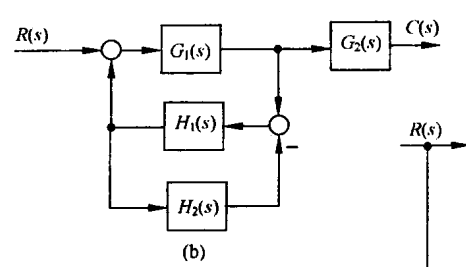
图c
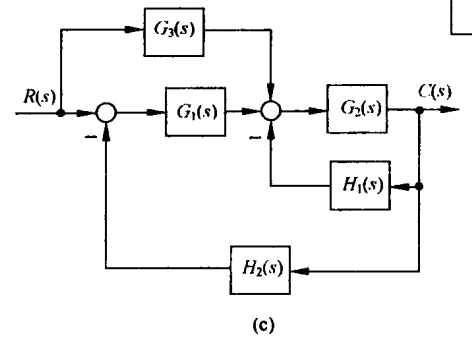
图d
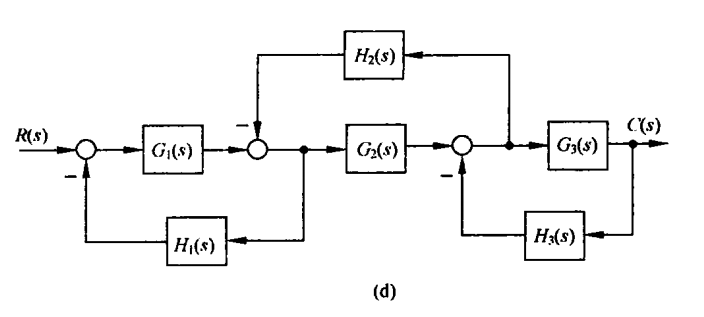
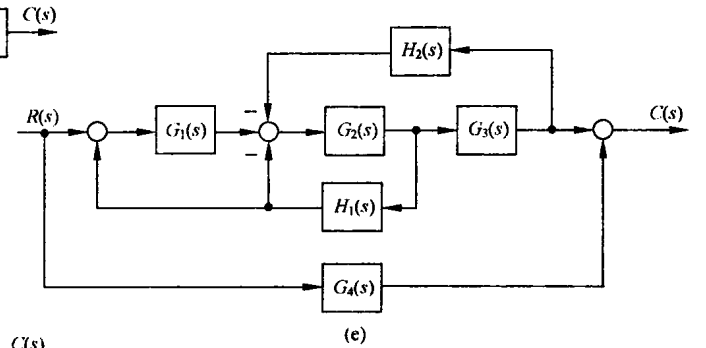
图e
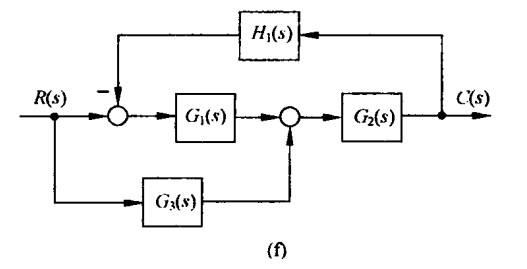
图f
关键点
知识点窍:结构图等效变换
逻辑推理:结构图等效变换的3种基本运算形式为:串联等效、并联等效和反馈连接等效。结构图的等效变换规则如表2-1所示。
解题过程
图a

图2-17(a)所示的等效变换(简化)过程如图2-18(a)所示。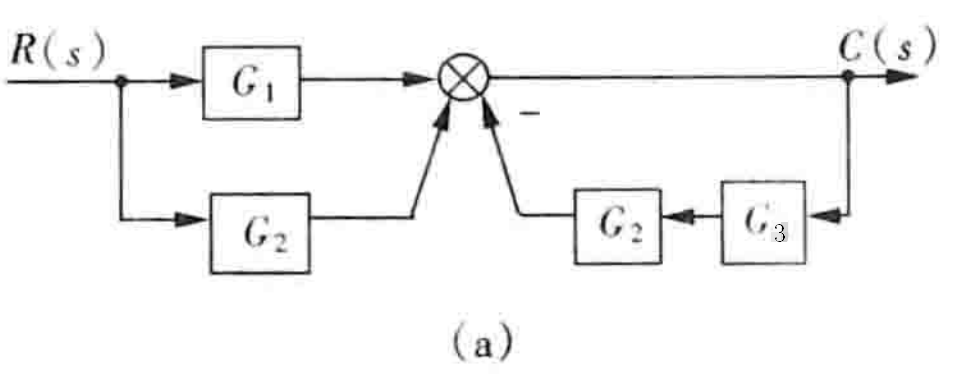
再次等效变换如下: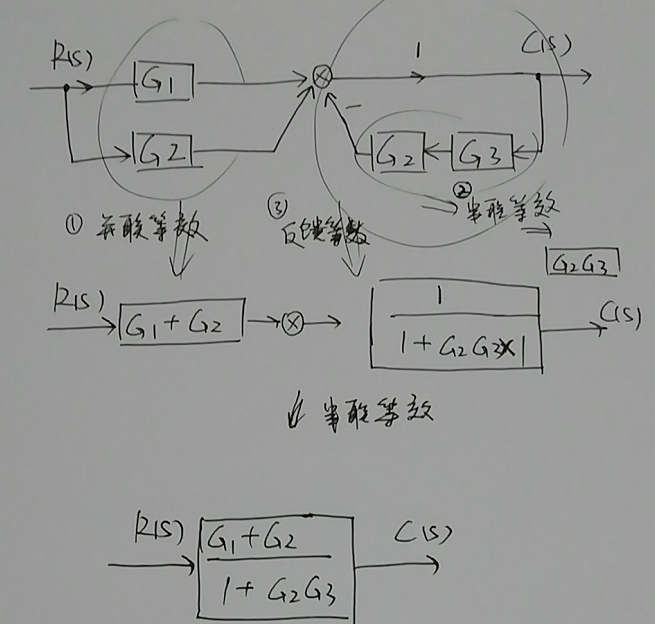
答案a
由此可得,系统传递函数为:
$\dfrac{C(s)}{R(s)}=\dfrac{G_1+G_2}{1+G_2G_3}$
图b

观察图b,可以看出$H_1(s)$和$H_2(s)$构成了一个负反馈: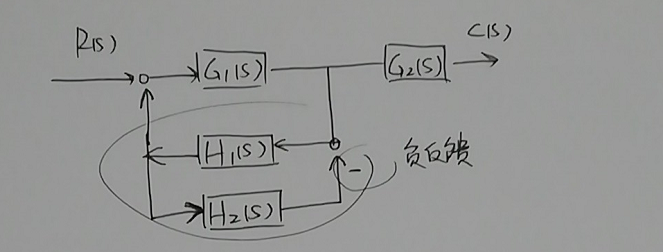
所以可以进行反馈等效如下图所示: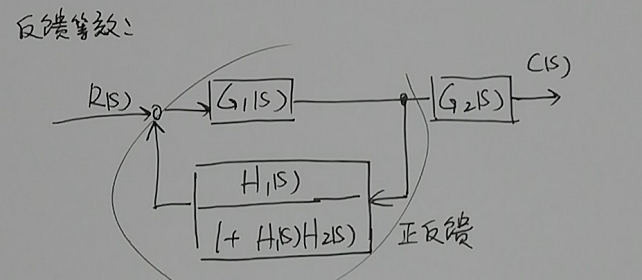
继续观察,发现$H_1(s)$和$H_2(s)$等效的框图(设为$G_3(s)$)和$G_1(s)$构成了一个正反馈,等效框图如下图: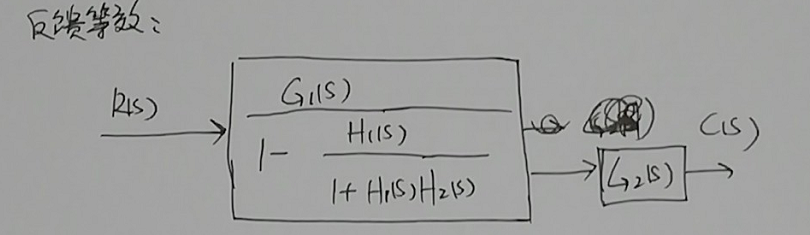
再次化简,得到等效框图如下图所示: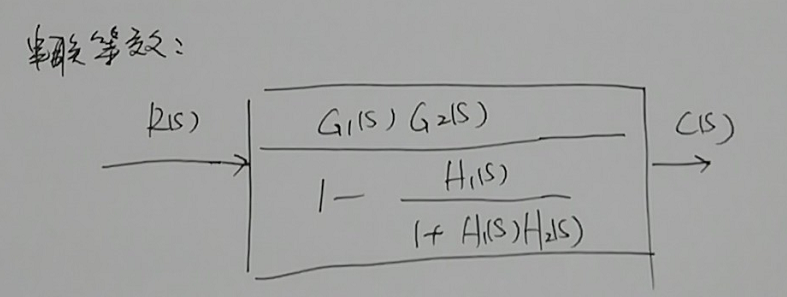
所以传递函数为:
$\dfrac{C(s)}{R(s)}=\dfrac{G_1(s)G_2(s)}{1-\dfrac{H_1(s)}{1+H_1(s)H_2(s)}}$
整理得到:
答案b
$$
\begin{aligned}
\dfrac{C(s)}{R(s)}=&\dfrac{G_1(s)G_2(s)}{1-\dfrac{H_1(s)}{1+H_1(s)H_2(s)}} \\
=&\dfrac{G_1(s)G_2(s)[1+H_1(s)H_2(s)]}{1+H_1(s)H_2(s)-H_1(s)} \\
\end{aligned}
$$
图c

把$H_2$的输出移动到$G_1$和$G_2$之间: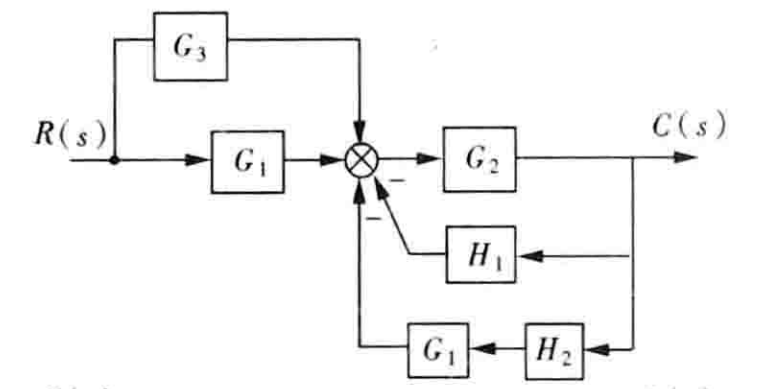
合并两个并联的框图$G_1,G_3$和$G_1,H_2,H_1$: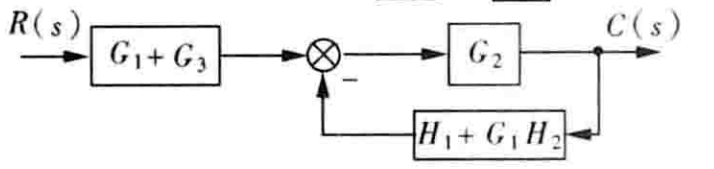
合并反馈框图:
所以系统的传递函数为:
$\dfrac{C(s)}{R(s)}=\dfrac{G_2(G_1+G_3)}{1+G_2(H_1+G_1H_1)}$
图d

把$H_2$的输入移动到$G_3$后面,移动后以多引入一个$G_3$的信号,所以要除去该信号.把$H_2$的输出移动到$G_1$前面,同样要除以$G_1$: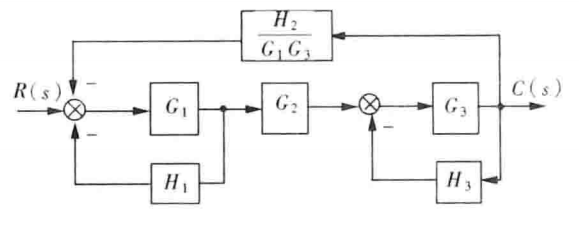
合并两个反馈回路: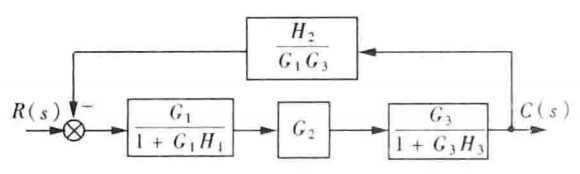
合并串联框图得到$G_5$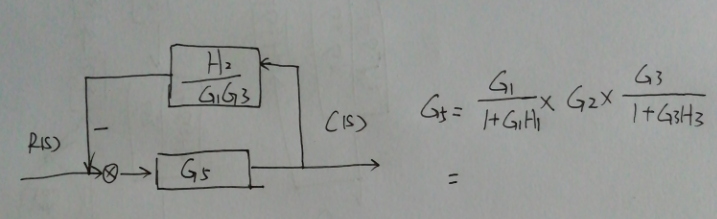
$G_5$的传递函数为:
$$
\begin{aligned}
G_5=&\dfrac{G_1}{1+G_1H_1}\times G_2\times\dfrac{G_3}{1+G_3H_3} \\
=&\dfrac{G_1(1+G_3H_3)+G_2(1+G_1H_1)(1+G_3H_3)+G_3(1+G_1H_1)}{(1+G_1H_1)(1+G_3H_3)} \\
=&\dfrac{G_1+G_1G_3H_3+G_2+G_2G_3H_3+G_2G_1H_1+G_2G_1H_1G_3H_3+G_3+G_3G_1H_1}{1+G_3H_3+G_1H_1+G_1H_1G_3H_3} \\
=&\dfrac{G_1+G_2+G_3+G_1G_3H_3+G_2G_3H_3+G_1G_2H_1+G_1G_3H_1+G_1G_2G_3H_1H_3}{1+G_1H_1+G_3H_3+G_1H_1G_3H_3} \\
\end{aligned}
$$
等效框图如下: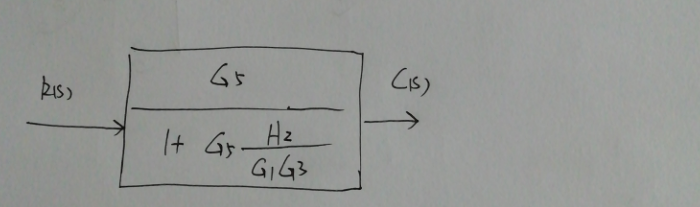
答案
代入$G_5$进行,整理可得:
$\dfrac{C(s)}{R(s)}=\dfrac{G_1G_2G_3}{1+G_1H1+G_2H2+G_3H_3+G_1H_1G_3H_3}$
图e

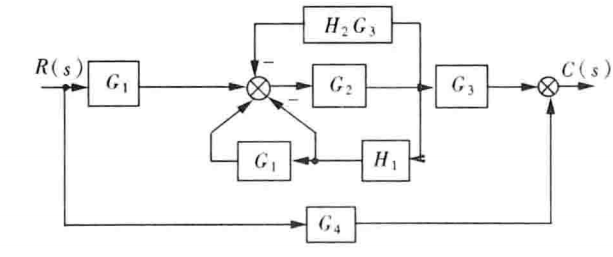
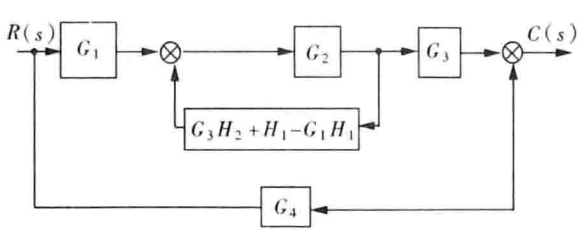
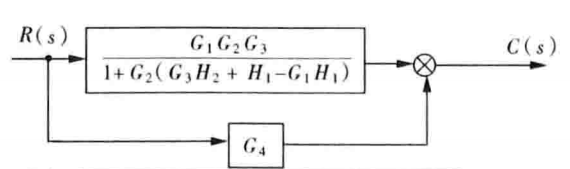

答案
所以系统传递函数为:
$\dfrac{C(s)}{R(s)}=\dfrac{G_4+G_1G_2G_3}{1+G_2G_3H_2+G_2H_1-G_1G_2H_1}$
图f

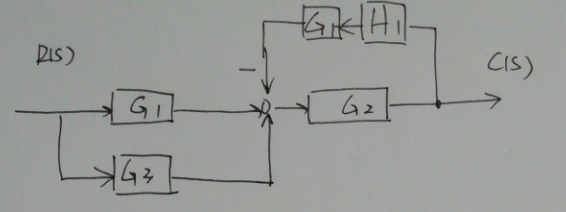
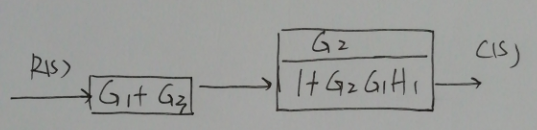
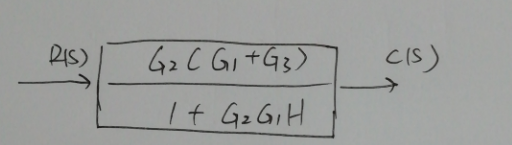
答案
$\dfrac{C(s)}{R(s)}=\dfrac{G_2(G_1+G_3)}{1+G_1G_2H_1}$
原文链接: 自动控制原理 作业题 2-17

