1-1函数

• 要求
• 填空题
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
• Latex语法
  • 多行公式等号对齐
  • 多行公式不自动编号
• 参考链接

要求

理解分段函数，复合函数，初等函数，反函数，隐函数的概念与特性

填空题

1

设$f(x)$为奇函数，且当$x\ge 0$ 时，$f(x)=\sqrt{x}$，则当$x \lt 0$时，$f(x)=?$查看答案。

奇函数是指对于一个定义域关于原点对称的函数$f(x)$的定义域内任意一个x，都有$f(-x)= - f(x)$，那么函数$f(x)$就叫做奇函数（odd function）。

解

因为$f(-x)= - f(x)$，所以$-f(-x)=f(x)$,即$f(x)=-f(-x)=-\sqrt{-x}$

2

函数 $f(x)=\sqrt{3-x}+arctan\dfrac{1}{x}$的定义域是？答案

具体函数定义域的求法

• 如果f(x)是整式,那么函数的定义域是实数集R;
• 如果f(x)是分式$f(x)=\dfrac{x}{y}$,那么函数的定义域是使分母不等于零的实数的集合,$y\not=0$;
• 如果f(x)是偶次根式$f(x)=\sqrt[n]{x}$,$n$为偶数那么函数的定义域是使根号内的式子大于或等于零的实数的集合;
• 如果f(x)中含有0次幂因式,$f(x)=x^0$,则要求0次幂的底数不为0,$x\not=0$;
• 如果f(x)是由几部分数学式子构成的,那么函数的定义域是使各部分式子都有意义的实数集合;(即求各集合的交集)
• 如果f(x)是由实际问题抽象出来的函数,则函数的定义域满足实际问题有意义。
  参考https://wenku.baidu.com/view/a778001a182e453610661ed9ad51f01dc28157c6.html?from=search

解
$$\begin{cases} 3-x \ge 0,\Rightarrow x\le3\\ x \not= 0\\ \end{cases}$$

所以定义域为$\{x|x\le3,且x\not=0\}$.

3

函数$f(x)=ln(\sqrt{1+x^2}-x)$的奇偶性为?(答案：奇函数)

解
首先看定义域，定义域关于原点对称才有奇偶性。
$$\begin{cases} \sqrt{1+x^2}-x>0,\Rightarrow\sqrt{1+x^2}>x\Rightarrow\{x=|x\in R\}\\ 1+x^2>=0,\rightarrow\{x=|x\in R\} \end{cases}$$

可以看到定义域为R，定义域关于原点对称。
$$\begin{align} f(-x)&=ln(\sqrt{1+(-x)^2}-(-x))\nonumber\\ &=ln(\sqrt{1+x^2}+x)\nonumber \end{align}$$

$$\begin{align} f(-x)+f(x)&=ln(\sqrt{1+x^2}+x)+ln(\sqrt{1+x^2}-x)\nonumber\\ &=ln[(\sqrt{1+x^2}+x)(\sqrt{1+x^2}-x)]\nonumber\\ &=ln(1+x^2-x^2)\nonumber\\ &=ln1\nonumber\\ &=0\nonumber \end{align}$$

所以$f(x)=-f(-x)$,所以，是奇函数。
答案1: https://www.zybang.com/question/1bfb772c63236322c8053d66d7bdeade.html
答案2：https://www.zybang.com/question/b4d4975533597237fa43d86f9ee1dc44.html

如何判断一个函数的奇偶性 一共有几种方法
1、奇函数、偶函数的定义中,首先函数定义域D关于原点对称.它们的图像特点是：
奇函数的图像关于原点对称,偶函数的图像关于X轴对称.
即$f(x)＝-f(-x)$为奇函数,$f(x)＝f(-x)$为偶函数$\Rightarrow f(x)+f(-x)=0$的是奇函数，$f(x)-f(-x)=0$的是偶函数
2、判断函数的奇偶性大致有下列二种方法：
(1)用奇、偶函数的定义,主要考察f(-x)是否与-f(x) ,f(x) ,相等.
(2)利用一些已知函数的奇偶性及下列准则：

• 两个奇函数的代数和是奇函数；相同相加相同
• 两个偶函数的代数和是偶函数；
• 奇函数与偶函数的和既非奇函数,也非偶函数；相异相加全不是
• 两个奇函数的乘积是偶函数；相同相乘是偶
• 两个偶函数的乘积是偶函数；
• 奇函数与偶函数的乘积是奇函数. 相异相乘是奇
  参考https://www.zybang.com/question/c2bb17b05b643ec99318cd9b79f92c89.html
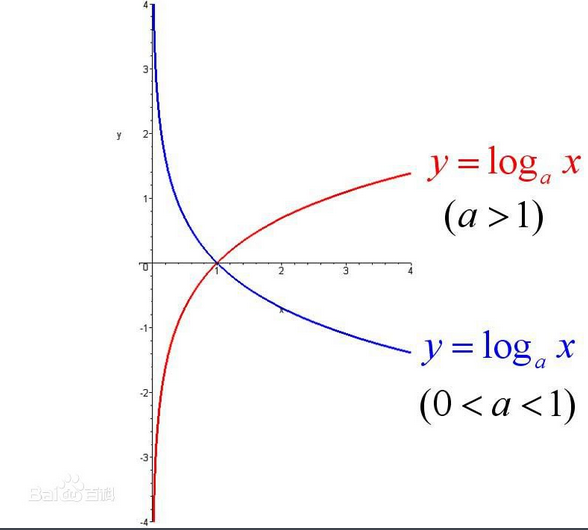
  对数公式https://blog.csdn.net/flyawayl/article/details/78946137
  $log_aM^n=nlog_aM$
  ${log_a}{\frac{M}{N}}=log_aM-log_aN$

4

设$g(x)=\dfrac{2^x}{2^x+1}$，则其反函数$g^{-1}(x)=$? 答案
解
由已知
$$\begin{align} 由(2^x+1)y&=2^x \nonumber \\ \Rightarrow 2^xy+y&=2^x \nonumber \\ \Rightarrow 2^xy-2^x&=-y \nonumber \\ \Rightarrow 2^x(y-1)&=-y \nonumber \\ \Rightarrow 2^x&=\dfrac{-y}{y-1} \nonumber \\ \Rightarrow x&=log_2\dfrac{-y}{y-1} \nonumber \\ \Rightarrow x&=log_2\dfrac{y}{1-y} \nonumber \\ \Rightarrow y&=log_2\dfrac{x}{1-x} \nonumber \\ \end{align}$$
下面来求定义域，$\begin{cases} \dfrac{x}{1-x}>0 \\ 1-x\not=0\Rightarrow x\not=1 \end{cases}$
由$\dfrac{x}{1-x}>0$得：$\begin{cases} x>0 \\ 1-x>0 \end{cases}$或者$\begin{cases} x<0 \\ 1-x<0 \end{cases}$
也就是$x(1-x)< 0$,令$x(1-x)= 0$,解得$\Rightarrow x_1=0,x_2=1$,$\Rightarrow x\in (0,1)$.

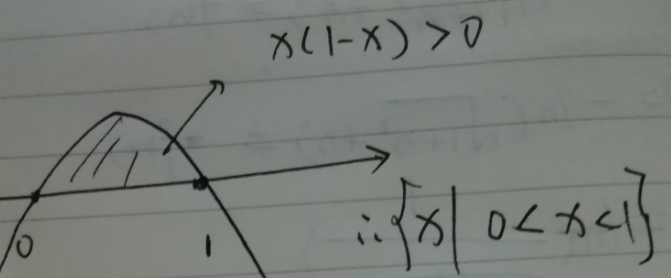
答案为:$log_2\dfrac{x}{1-x},x\in (1,0)$

y=ax²+bx+c
一元二次方程的开口方向由a的符号决定.
a>0 开口向上
a < 0 开口向下
一元二次方程开口方向
参考链接https://zhidao.baidu.com/question/245373105415112764.html

5

设$f(x-\dfrac{1}{x})=x^2+\dfrac{1}{x^2}$,则$f(x)=$? 答案
$(x-\dfrac{1}{x})^2=x^2-2x\dfrac{1}{x}+\dfrac{1}{x^2}=x^2+\dfrac{1}{x^2}-2$
所以，$x^2+\dfrac{1}{x^2}=(x-\dfrac{1}{x})^2+2$，所以$f(x-\dfrac{1}{x})=(x-\dfrac{1}{x})^2+2$，所以
$f(x)=x^2+2$

完全平方公式即$\begin{cases} (a+b)^2=a^2+2ab+b^2 \\ (a-b)^2=a^2-2ab+b^2 \end{cases}$

6

若$y=f(u)=e^u$,$u=g(v)=-v^2$,$v=h(w)=sinw$,
$w=\varphi(x)=\dfrac{1}{x}$,则复合函数$y=f(g(h(\varphi(x))))=$?
解
$h(\varphi(x))=sin\dfrac{1}{x}$,$g(h(\varphi(x))=-(h(\varphi(x))^2=-sin^2\dfrac{1}{x}$,
所以：$y=e^{-sin^2\dfrac{1}{x}}$

Latex语法

多行公式等号对齐

\begin{align}
  (a + b)^3  &= (a + b) (a + b)^2        \\
             &= (a + b)(a^2 + 2ab + b^2) \\
             &= a^3 + 3a^2b + 3ab^2 + b^3
\end{align}

效果：
$$\begin{align} (a + b)^3 &= (a + b) (a + b)^2 \\ &= (a + b)(a^2 + 2ab + b^2) \\ &= a^3 + 3a^2b + 3ab^2 + b^3 \end{align}$$

多行公式不自动编号

在公式后面换行符\\之前添加\nonumber即可。

$$
\begin{align}
f(-x)&=ln(\sqrt{1+(-x)^2}-(-x))\nonumber\\
	&=ln(\sqrt{1+x^2}+x)\nonumber
\end{align}
$$

$$\begin{align} f(-x)&=ln(\sqrt{1+(-x)^2}-(-x))\nonumber\\ &=ln(\sqrt{1+x^2}+x)\nonumber \end{align}$$

参考链接

Latex中使用align来对齐多行公式的排版技巧
LaTex集合之间关系表示
完全平方公式

本文链接: 1-1函数