测验1
题1

解:令$u(x)=\dfrac{1}{x}$,则$\lim \limits_{x \to 0^+ }u(x)=\lim \limits_{x \to 0^+ }\dfrac{1}{x}=+\infty$
所以:$\lim \limits_{x \to 0^+ }arctan\dfrac{1}{x}=\lim \limits_{u(x) \to +\infty }arctan(u(x) )=\dfrac{\pi}{2}$
$tanx$为初等函数,所以极限值等于函数值,即$\lim \limits_{x \to 0^+ }tanx=tan(0)=0$
由cotx函数的图像可得:
$\lim \limits_{x \to 0^+ }cotx=+\infty$
x是无穷小量,cosx是有界函数,无穷小量与有界函数的乘积是无穷小量,所以
$\lim \limits_{x \to 0^+ }xcosx=0$
题2

题3

$\lim \limits_{x \to 0^+ }\dfrac{1}{x}=+\infty$
题4

解:$\lim \limits_{x \to 4 }x-4=0$,则分子中能消去$x-4$这个零因子,
设$x^2-3x+c=(x-4)(x+b)$
则
$$
\begin{align}
&\lim \limits_{x \to 4 }\dfrac{x^2-3x+c}{x-4} \nonumber \\
=&\lim \limits_{x \to 4 }\dfrac{(x-4)(x+b)}{x-4} \nonumber \\
=&\lim \limits_{x \to 4 }(x+b) \nonumber \\
=&5 \nonumber \\
\end{align}
$$
解得$b=1$,所以
$$
\begin{align}
&x^2-3x+c \nonumber \\
=&(x-4)(x+1) \nonumber \\
=&x^2-3x-4 \nonumber \\
\end{align}
$$
所以$c=-4$
题5

题6

题7
题8

不知道为什么
题9

$\lim \limits_{x \to \infty }\dfrac{x}{x^3+1}=0$,$|sinx|\le 1$,
所以$\lim \limits_{x \to \infty }\dfrac{x}{x^3+1}sinx=0$,有界函数与无穷小的乘积依然是无穷小。
题10

解:这是一个0比0型极限
因为:$x^2+3x-4=(x-1)(x+4)$,$x^2-1=(x+1)(x-1)$
$$
\begin{align}
\text{原式}=&\lim \limits_{x \to 1 }\dfrac{(x-1)(x+4)}{(x+1)(x-1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(x+4)}{(x+1)} \nonumber \\
=&\dfrac{5}{2} \nonumber \\
\end{align}
$$
测验2
题1

$\lim \limits_{x \to 0^+ }\frac{1}{x}=+\infty$
$\lim \limits_{x \to 0^+ }arctan\dfrac{1}{x}=\dfrac{\pi}{2}$ 不是无穷小,所以排除A
$\lim \limits_{x \to 0^+ }cotx=+\infty$,排除B
由反余切函数图像可知
$\lim \limits_{x \to 0^+ }arccotx=\dfrac{\pi}{2}$ 排除D
x是无穷小,$|cos\dfrac{1}{x}| \le 1$,所以
$\lim \limits_{x \to 0^+ }xcos\dfrac{1}{x}=0$
题2

$x to 0^+$,函数$ln(x-1)$定义域为 $\{x|x>1\}$,$\{x|x>1\}ln(x-1)$不存在
$\lim \limits_{x \to 0+ } \dfrac{1}{x}cos\dfrac{1}{x}=+\infty$
$\lim \limits_{x \to 0^+ }lnx=+\infty$ 所以$x \to 0^+$时$lnx$为无穷大量,根据无穷大量与无穷小量的关系得:$x \to 0^+$时 $\dfrac{1}{lnx}$为无穷小量
题3

题4

题5

解 $x^2-1=(x+1)(x-1)$
所以$
y=\dfrac{(x+1)(x-1)}{x-1}e^{\dfrac{1}{x-1}}
=(x+1)e^{\dfrac{1}{x-1}}
$
所以 $\lim \limits_{x \to -1 }(x+1)e^{\dfrac{1}{x-1}}=0$
题6

$\lim \limits_{x \to 4 }x-4=0$,所以肯定能消掉这个零因子。
令$\lim \limits_{x \to 4 }\dfrac{(x-4)(x+b)}{x-4}=\lim \limits_{x \to 4 }x+b=5$,解得b=1.
$(x-4)(x+1)=x^2-3x-4=x^2-3x+c$,所以$c=-4$
题7

背
题8

题9

因为$x^2+3x-4=(x-1)(x+4)$,$x^1-1=(x+1)(x-1)$
所以$\lim \limits_{x \to 1 } \dfrac{(x-1)(x+4)}{(x+1)(x-1)}=\lim \limits_{x \to 1 } \dfrac{(x+4)}{(x+1)}=\dfrac{5}{2}$
题10

解:这是一个等比数列
公比:$q=\dfrac{a_{n+1}}{a_n}=\dfrac{\dfrac{1}{2}}{1}=\dfrac{1}{2}$
前n项和:
$$
\begin{align}
S_n=&\dfrac{a_1(1-q^n)}{1-q} \nonumber \\
=&\dfrac{1(1-(\dfrac{1}{2})^n)}{1-\dfrac{1}{2}} \nonumber \\
=&\dfrac{(1-(\dfrac{1}{2})^n)}{\dfrac{1}{2}} \nonumber \\
=&2(1-(\dfrac{1}{2})^n) \nonumber \\
\end{align}
$$
$\lim \limits_{n \to \infty }\dfrac{1}{2}=0$
所以$\lim \limits_{n \to \infty }2(1-(\dfrac{1}{2})^n)=2$
测试3
题2

题3

题5

题4

题6

题7

题8
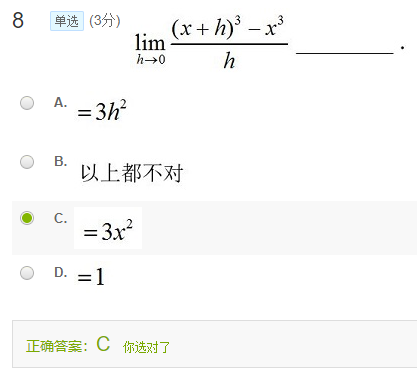
题9

这题分子是个等差数列
前n项和公式:
$S_n=\dfrac{n(a_1+a_n)}{2}=na_1+\dfrac{n(n-1)}{2}d$
公差
$S_n=\dfrac{n(1+n-1)}{2}=\dfrac{n^2}{2}$
$$
\begin{align}
&\lim \limits_{x \to \infty }\dfrac{1+2+3+\cdots+(n-1)}{n^2} \nonumber \\
=&\lim \limits_{x \to \infty }\dfrac{\dfrac{1}{2}n^2}{n^2} \nonumber \\
=&\dfrac{1}{2} \nonumber \\
\end{align}
$$
测验4
题3
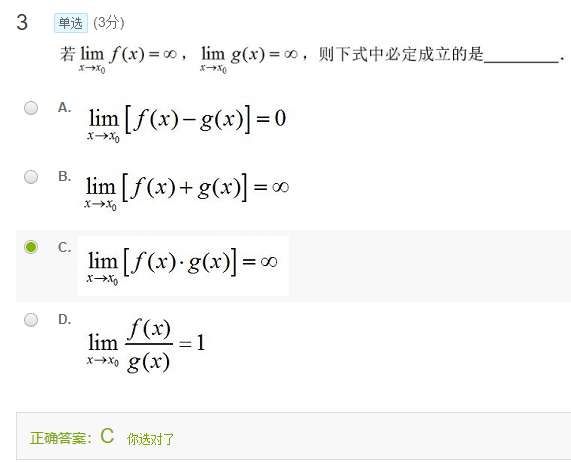
题4

题6

本文链接: 第二讲 测验


