前言
系统的稳态性能反映系统跟踪控制信号的准确度或抑制扰动信号的能力,这种能力用稳态误差来描述。
在系统的分析、设计中,稳态误差是一项重要的性能指标,它与系统本身的结构、参数及外作用的形成有关,也与元件的不灵敏、零点漂移、老化及各种传动机械的间隙、摩擦等因素有关。
稳态误差分类
- 给定值稳态误差(由给定输入引起的稳态误差)
- 扰动值稳态误差(由扰动输入引起的稳态误差)
对于随动系统,给定输入变化,要求系统输出量以一定的精度跟随输入量的变化,因而用给定稳态误差来衡量
系统的稳态性能。
对恒值系统,给定输入通常是不变的,需要分析输出量在扰动作用下所受到的影响,因而用扰动稳态误差来衡
量系统的稳态性能。
本文介绍稳态误差的概念和计算方法,研究稳态误差的规律性。
稳态误差的定义
系统的误差$e(t)$一般定义为输出量的希望值与实际值之差。对图示典型系统,其误差定义有两种形式:
从系统输出端定义
$e(t)=c_r(t)-c(t)$
式中,$c_r(t)$为系统输出量的希望值,$c(t)$为输出量的实际值。在性能指标提法中经常使用,但在实际系统中无法测量,因而,一般只有数学意义。
从输入端定义
$e(t)=r(t)-b(t)$
系统输出量的希望值是给定输入$r(t)$,输出量的实际值为系统主反馈信号$b(t)$。通常$H(s)$是测量装置的传递函数,此时误差是给定输入与测量装置输出量之差。$b(t)$可以测量,因而具有实用性。
第二种形式的误差是从系统的输入端来定义的,它在系统中是可以测量的,因而具有实用性。
对于单位反馈系统,要求输出量$C(t)$的变化规律与给定输入r(t)的变化规律完全一致,所以给定输入r(t)也就是
输出量的希望值$C_r{t}$,即C_r(t)=r(t) 。此时,上述两种定义统一为:
$e(t)= r(t)-c(t)$
从本质上看,两种定义的误差都能反映控制系统的控制精度。在下面的讨论中,采用第二种误差定义。
$e(t)$通常也称为系统的误差响应,它反映了系统在输入信号和扰动信号作用下整个工作过程中的精度。
误差响应组成
误差响应中也包含有瞬态分量和稳态分量两个部分,如果所研究的系统是稳定的,那么当时间$t$趋于无穷大时,瞬态分量趋近于零,剩下的只是稳态分量。
稳态误差的定义
稳定系统 误差信号的稳态分量称为系统的稳态误差,以$e_ss$表示。
e_ss=$\lim \limits_{t\to \infty}e(t)$
误差:是参考输入信号和反馈信号的差值
$e(t)=r(t)-b(t)$
误差的拉氏变换
$E(s)=\dfrac{1}{1+G(s)H(s)}R(s)$
稳态误差:
$e_{ss}=e(\infty)=\lim \limits_{t \to \infty }e(t)=\lim \limits_{t \to \infty }[r(t)-b(t)]$
注
- 这种定义为缺省定义,对于其它定义的稳态误差,必须首先给出误差的定义式。
- 对于稳定的系统,才有稳态误差的概念;
- 稳态误差与系统的结构参数和输入的形式有关。因此在规定稳态误差的要求时,需要指明输入信号的类型。衡量标准是用一些典型输入信号作为标准。
系统的开环传递函数
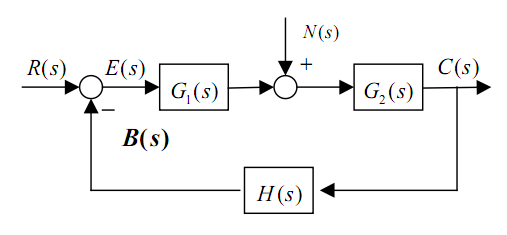
上图中将反馈的输出通路断开,反馈信号对于参考输入信号的传递函数称为开环传递函数(反馈除以输入)。这时前向通路传递函数与反馈通路传递函数的乘积为该系统的开环传递函数。
$G(s)=\dfrac{B(s)}{R(s)}=G_1(s)G_2(S)H(s)$
典型反馈控制系统
典型反馈控制系统如下图所示:
r(t)作用下的给定稳态误差
由于线性系统满足叠加性,设扰动输入$n(t)=0$,系统的结构图的到简化如下: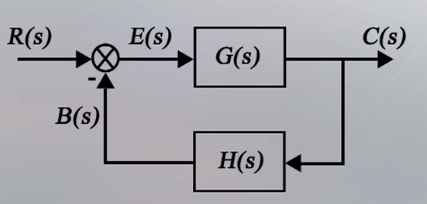
由图可知:$\dfrac{C(s)}{R(s)}=\dfrac{G(s)}{1+G(s)H(s)}$
所以$C(s)=R(s)\dfrac{G(s)}{1+G(s)H(s)}$
由误差的定义可知:
$E(s)=R(s)-B(s)=R(s)-C(s)H(s)$,
代入$C(s)=R(s)\dfrac{G(s)}{1+G(s)H(s)}$可得:
$$
\begin{aligned}
E(s)=&R(s)-B(s) \\
=&R(s)-C(s)H(s) \\
=&R(s)-R(s)\dfrac{G(s)}{1+G(s)H(s)}H(s) \\
=&\dfrac{1}{1+G(s)H(s)}R(s) \\
=&\varPhi_{er}R(s)
\end{aligned}
$$给定输入作用下系统的误差传递函数:
$\varPhi_{er}=\dfrac{1}{1+G(s)H(s)}$
稳态误差
$e_{ssr}=\lim \limits_{t \to \infty}e(t)=\lim \limits_{t \to \infty}sE(s)$,代入$E(s)=\dfrac{1}{1+G(s)H(s)}R(s) $得到:
$$
\begin{aligned}
e_{ssr}=&\lim \limits_{t \to \infty}e(t) \\
=&\lim \limits_{s \to 0}sE(s) \\
=&\lim \limits_{s \to 0}\dfrac{sR(s)}{1+G(s)H(s)} \\
\end{aligned}
$$
开环传递函数G(s)H(s)的时间常数形式
$$
\begin{aligned}
G(s)H(s)=&\dfrac{K(1+\tau_1s)(1+\tau_2s)\cdots(1+\tau_ms)}{s^v(1+T_1s)(1+T_2s)\cdots(1+T_{n-v}s)} \\
=&\dfrac{K\prod\limits_{j=1}^{m}(\tau_js+1)}{s^v\prod\limits_{i=1}^{n-v}(T_is+1)} \\
\end{aligned}
$$
式中:
$K=\lim\limits_{s\to 0}s^vG(s)H(s)$,称为系统的开环放大系数(开环增益)
$s^v$开环传递函数在原点处有重极点,或者说由$v$个积分环节串联
系统类型
对于开环传递函数为:
$$
\begin{aligned}
G(s)H(s)=&\dfrac{K(1+\tau_1s)(1+\tau_2s)\cdots(1+\tau_ms)}{s^v(1+T_1s)(1+T_2s)\cdots(1+T_{n-v}s)} \\
=&\dfrac{K\prod\limits_{j=1}^{m}(\tau_js+1)}{s^v\prod\limits_{i=1}^{n-v}(T_is+1)} \\
\end{aligned}
$$
的系统:
- 当$v=0$时,称该系统为$0$型系统
- 当$v=1$时,称该系统为$1$型系统
- 当$v=2$时,称该系统为$2$型系统
输入作用下的稳态误差
单位阶跃输入时的稳态误差
单位阶跃输入$R(s)=\dfrac{1}{s}$,代入稳态误差的基本公式:
$$
\begin{aligned}
e_{ssr}=&\lim \limits_{t \to \infty}e(t) \\
=&\lim \limits_{s \to 0}sE(s) \\
=&\lim \limits_{s \to 0}\dfrac{s}{1+G(s)H(s)}R(s) \\
\end{aligned}
$$
求得系统的稳态误差
$$
\begin{aligned}
e_{ssr}=&\lim \limits_{s \to 0}\dfrac{s}{1+G(s)H(s)}\dfrac{1}{s} \\
=&\lim \limits_{s \to 0}\dfrac{1}{1+G(s)H(s)} \\
=&\dfrac{1}{1+\lim \limits_{s \to 0}G(s)H(s)} \\
\end{aligned}
$$
稳态位置误差系数
稳态位置误差系数$K_p=\lim \limits_{s \to 0}G(s)H(s) $,则稳态误差:
稳态误差表达式
$e_{ssr}=\dfrac{1}{1+K_p}$
可以看到稳态误差$e_{ssr}$只与稳态位置误差系数$K_p$有关
不同类型下的稳态误差
0型系统
0型系统就是$v=0$的系统,此时:
稳态位置误差系数$K_p=K(\text{开环放大系数})$
稳态误差$e_{ssr}=\dfrac{1}{1+K}$,可以看到$e_{ssr}$反比于开环放大系数$K$,当开环放大系数$K$增大时,$e_{ssr}$减少
称这样的系统为有差系统
1型或高于1型系统
也就是$v>=1$的系统,此时:
稳态位置误差系数$K_p=\infty$
稳态误差$e_{ssr}=0$
称这样的系统为无差系统
单位斜坡输入时的稳态误差
代入单位斜坡信号:$R(s)=\dfrac{1}{s^2}$,即可得到:
系统稳态误差
$$
\begin{aligned}
e_{ssr}=&\lim \limits_{s \to 0}\dfrac{s}{1+G(s)H(s)}R(s) \\
=&\lim \limits_{s \to 0}\dfrac{s}{1+G(s)H(s)}\times\dfrac{1}{s^2} \\
=&\lim \limits_{s \to 0}\dfrac{1}{s+sG(s)H(s)} \\
=&\dfrac{1}{\lim \limits_{s \to 0}s+\lim \limits_{s \to 0}sG(s)H(s)} \\
=&\dfrac{1}{\lim \limits_{s \to 0}sG(s)H(s)} \\
\end{aligned}
$$
稳态速度误差系数
定义稳态速度误差系数为:$K_v=\lim \limits_{s \to 0}sG(s)H(s)$
稳态误差表达式
所以系统稳态误差为:
$e_{ssr}=\dfrac{1}{K_v}$
不同系统类型下的稳态误差
0型系统
代入开环传递函数:
$G(s)H(s)=\dfrac{K\prod\limits_{j=1}^{m}(\tau_js+1)}{s^v\prod\limits_{i=1}^{n-v}(T_is+1)}$
得到,0型系统($v=0$)的稳态速度误差系数:
$$
\begin{aligned}
K_v=&\lim \limits_{s \to 0}sG(s)H(s) \\
=&\lim\limits_{s \to 0}s\times \dfrac{K\prod\limits_{j=1}^{m}(\tau_js+1)}{s^0\prod\limits_{i=1}^{n}(T_is+1)} \\
=&0
\end{aligned}
$$
0型系统稳态误差
此时,得到0型系统的稳态误差:
$e_{ssr}=\dfrac{1}{K_v}=\infty$
1型系统
1型系统($v=1$),稳态速度误差系数:
$$
\begin{aligned}
K_v=&\lim \limits_{s \to 0}sG(s)H(s) \\
=&\lim\limits_{s \to 0}s\times \dfrac{K\prod\limits_{j=1}^{m}(\tau_js+1)}{s\prod\limits_{i=1}^{n}(T_is+1)} \\
=&K
\end{aligned}
$$
1型系统稳态误差
所以1型系统稳态误差:
$e_{ssr}=\dfrac{1}{K_v}=\dfrac{1}{K}$
2型及以上系统
$v\ge 2$,稳态速度误差系数:
$$
\begin{aligned}
K_v=&\lim \limits_{s \to 0}sG(s)H(s) \\
=&\lim\limits_{s \to 0}s\times \dfrac{K\prod\limits_{j=1}^{m}(\tau_js+1)}{s^v\prod\limits_{i=1}^{n}(T_is+1)} \\
=&\infty
\end{aligned}
$$
2型及以上系统稳态误差
所以,2型及以上系统稳态误差:
$e_{ssr}=\dfrac{1}{K_v}=0$
单位抛物线输入时稳态误差
单位抛物线:$R(s)=\dfrac{1}{s^3}$,代入稳态误差公式
$$e_{ssr}=\lim\limits_{s\to 0}\dfrac{s}{1+G(s)H(s)}\times R(s)$$
得到:
$$
\begin{aligned}
e_{ssr}=&\lim\limits_{s\to 0}\dfrac{s}{1+G(s)H(s)}\times \dfrac{1}{s^3} \\
=&\dfrac{1}{\lim\limits_{s\to 0}s^2G(s)H(s)} \\
\end{aligned}
$$
稳态加速度误差
定义稳态加速度误差系数$K_a=\lim\limits_{s\to 0}s^2G(s)H(s)$
得到$e_{ssr}=\dfrac{1}{K_a}$
不同类型的稳态误差

不同输入信号下的的稳态误差汇总表
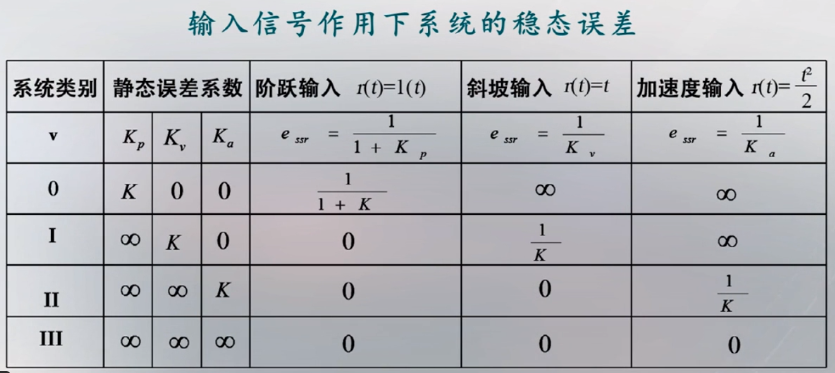
其中:
- $K$是开环放大系数
- 无差系统一定有积分环节,动态过程并不是无差。
- 要
减小稳态误差,增加开环增益$K$或积分环节数$v$($v\le 2$) - 若输入信号是多种典型输入的组合,则运用叠加原理。将各个稳态误差分量叠加起来。
汇总表2
课本(107页)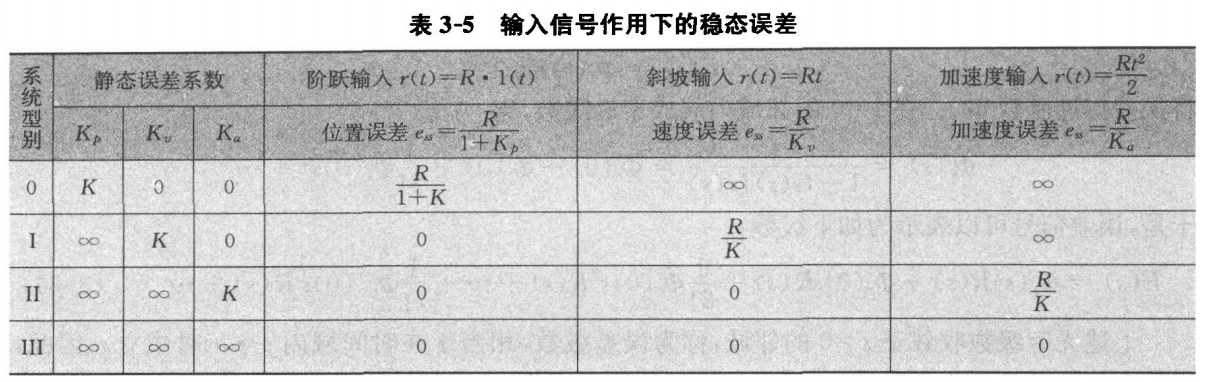
例题
若输入信号为$r(t)=A+Bt+$1 2$Ct^2$,则应用叠加原理可得稳态误差为:
$e_{ssr}=\dfrac{A}{1+K_p}+\dfrac{B}{k_v}+\dfrac{C}{K_a}$
扰动稳态误差的计算
控制系统除了受到给定输入的作用,通常还受到扰动输入的作用,给定输入作用的的稳态误差的计算可以看上述表.
典型控制系统结构图如下: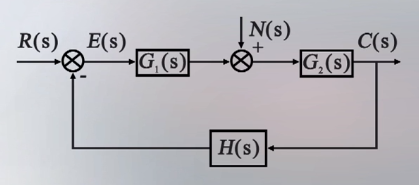
画出信号流入,利用梅森增益公式可求得N(s)到C(s)的传递函数:
$\dfrac{C(s)}{N(s)}=\dfrac{G_2(s)}{1+G_1(s)G_2(s)H(s)}$
得到$C(s)=\dfrac{G_2(s)}{1+G_1(s)G_2(s)H(s)}\times N(s)$
设给定输入$r(t)=0$($R(s)=0$),
由误差信号的定义得到:
$E(s)=R(s)-B(s)=0-H(s)C(s)$
代入$C(s)$,得到:
$E(s)=-\dfrac{G_2(s)H(s)}{1+G_1(s)G_2(s)H(s)}\times N(s)
=\varPhi_{en}(s)N(s)$
$\varPhi_{en}(s)$是扰动输入作用下系统的误差传递函数。
扰动输入作用下系统的误差传递函数
$\varPhi_{en}(s)=\dfrac{E(s)}{N(s)}=-\dfrac{G_2(s)H(s)}{1+G_1(s)G_2(s)H(s)}$
根据拉式变换的终值定理,得到扰动输入引起的稳态误差:
扰动稳态误差表达式
$$
\begin{aligned}
e_{ssn}=&\lim\limits_{t\to\infty} \\
=&\lim\limits_{s\to 0}-sE(s) \\
=&\lim\limits_{s\to 0}-\dfrac{sG_2(s)H(s)}{1+G_1(s)G_2(s)H(s)}\times N(s) \\
\end{aligned}
$$
例题
已知系统的结构图,问是否存在合适的$K_1$,使得系统在扰动信号$n(t)=1(t)$作用下的稳态误差$e_{ssm}=-0.099$?
解:标出节点: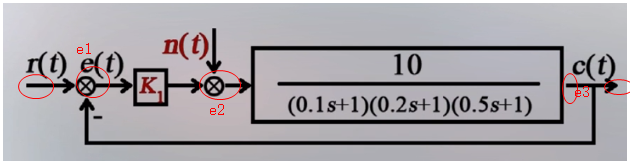
画出信号流图: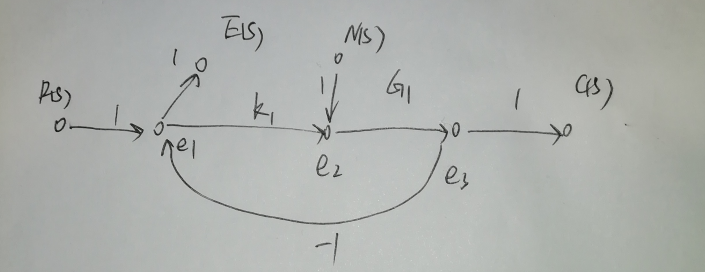
分析如下:
$G_1=\dfrac{10}{(0.1s+1)(0.2s+1)(0.5s+1)}$
$$
\begin{aligned}
\varPhi_{en}(s)=&\dfrac{E(s)}{N(s)} \\
=&\dfrac{-G_1}{1+K_1G_1} \\
=&\dfrac{-\dfrac{10}{(0.1s+1)(0.2s+1)(0.5s+1)}}{1+K_1\dfrac{10}{(0.1s+1)(0.2s+1)(0.5s+1)}} \\
=&\dfrac{-10}{(0.1s+1)(0.2s+1)(0.5s+1)+10K_1} \\
\end{aligned}
$$
对扰动信号$n(t)=1(t)$,取拉式变换得到:
$N(s)=\dfrac{1}{s}$
所以
$$
\begin{aligned}
E(s)=&\varPhi_{en}(s)N(s) \\
=&\dfrac{-10}{(0.1s+1)(0.2s+1)(0.5s+1)+10K_1}\dfrac{1}{s} \\
\end{aligned}
$$
根据终值定理得到稳态误差:
$$
\begin{aligned}
e_{ssn}=&\lim\limits_{s\to 0}sE(s) \\
=&\lim\limits_{s\to 0}s\dfrac{-10}{(0.1s+1)(0.2s+1)(0.5s+1)+10K_1}\dfrac{1}{s} \\
=&\lim\limits_{s\to 0}\dfrac{-10}{(0.1s+1)(0.2s+1)(0.5s+1)+10K_1} \\
=&\dfrac{-10}{1+10K_1}
\end{aligned}
$$
令$e_{ssn}=\dfrac{-10}{1+10K_1}=-0.099$
解得:$K_1=10$
由于稳态误差必须在系统稳定的情况下才有讨论的意义,所以还有判断系统的稳定性。
系统的特征方程为:
给定输入和扰动输入同时存在的情况
总稳态误差=给定稳态误差+扰动稳态误差

