概述
2-1时域教学模型
2-2复数城教学模型
2-3信号流图
概述
1、数学模型的定义
2、建立数学模型的意义
3、建立数学模型的方法
4、建立数学模型的工具
1、系统数学模型的定义
定义:描述系统内部物理量(或变量)之间关系的数学表达式称为数学模型。
物理模型:任何元件或系统实际上都是很复杂的,难以对它作出精确、全面的描述,必须进行简化或理想化。简化后的元件或系统为该元件或系统的物理模型。简化是有条件的,要根据问题的性质和求解的精确要求,来确定出合理的物理模型。
2、数学模型的意义
- 定量研究的基础
- 研究系统运行规律的基础
- 对系统行为进行控制的基础
- 对系统未来进行预测的基础
3、建立数学模型方法
解析法(分析法)
对系统各部分的运动机理进行分析,根据它们所依据的物理规律或化学规律运动数学知识分别列出相应的运行方程。
实验法
在系统内部关系复杂时,为达到某种目的,可以通过实验手段,测量该系统的输入输出,然后运用系统辨识的手段,构建出一个近似的数学模型。
实验法: 基于系统辨识的建模方法
已知知识和辨识目的
实验设计:选择实验条件
模型阶次:适合于应用的适当阶次
参数估计:最小二乘法
模型验证:将实际输出与模型的计算输出进行比较,系统模型需保证两个输出之间在选定意义上的接近
4、建立数学模型的数学工具
- 微分方程
- 差分方程
- 传递函数 拉氏变换传递函数,Z变换传递函数
- 其他数学工具(如 Rough Set, Petri等)
2-1 时域数学模型
1、线性元件的微分方程
2、线性系统的特性
3、非线性微分方程的线性化
4、线性定常微分方程的求解(拉氏变换法)
5、运动的模态(振型)
1、线性元件的微分方程
[例2-1] RLC 无源网络的微分方程,R:电阻 L:电感 C:电容
根据基尔霍夫电压定律
在任何闭合回路中,各元件上的电压降的代数和等于电动势的代数和,即从一点出发绕一周回到该点时,各段电压的代数和等于零。
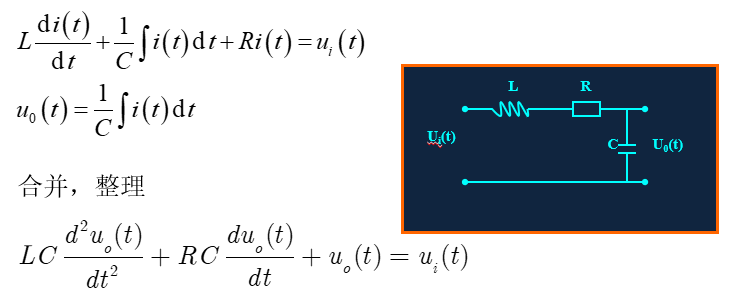
[例2-2] 求弹簧-阻尼-质量的机械位移系统的微分方程。输入量为外力F,输出量为位移x。
例2-1和例2-2的微分方程形式是完全一样的。
这是因为:若令$q=\int i dt$(电荷),则例2-1的结果变为: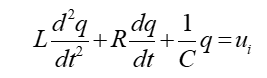
可见,同一物理系统有不同形式的数学模型,而不同类型的系统也可以有相同形式的数学模型。
作用与意义:利用相似系统的概念可以用一个易于实现的系统来模拟相对复杂的系统,实现仿真研究。
元件微分方程的建立
步1:根据元件的工作原理及其在控制系统中的作用,确定其输入量和输出量
步2:分析元件工作中所遵循的物理规律或化学规律,列写相应的微分方程
步3:消去中间变量,得到输出量与输入量之间关系的微分方程,便是元件时域的数学模型
控制系统微分方程的建立
步1:由原理图画出系统方框图
步2:写出组成系统各元件的微分方程
步3:消去中间变量便得到描述系统输出量与输入量之间的微分方程
2、线性系统的特性
在经典控制领域,主要研究的是线性 定常 控制系统。如果描述系统的数学模型是线性常系数的微分方程,则称该系统为线性定常系统,其最重要的特性便是可以应用线性叠加原理,即系统的总输出可以由若干个输入引起的输出叠加得到。
1) 线性系统的性质
- 可叠加性
- 均匀性(或奇次性)
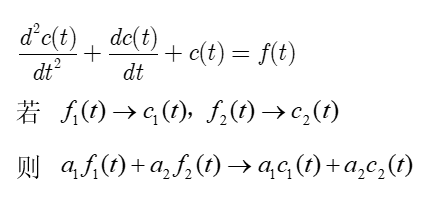
2、线性系统的特性
2) 线性系统性质的应用
- 多个外作用产生的响应可通过逐个外作用响应的
叠加。 零输入和零初始条件响应合成得到非零响应。- 系统对输入和干扰分别研究。
- 只有
线性时不变微分方程才能运用Laplace变换为代数方程。
后面要弄一个专门的拉氏变换表
3、非线性微分方程的线性化
问题:在实际工程中,几乎所有的器件、系统都是非线性的,完全线性的几乎没有。
解决方法:
(1) 许多情况下,在一定工作范围,一定精度范围下,可以近似看作是线性。
(2) 严重非线性情况下,在工作点附近,可以局部的线性化。
局部线性化-切线法(小偏差法)
基本步骤:
连续变化的非线性函数:
$y = f(x)$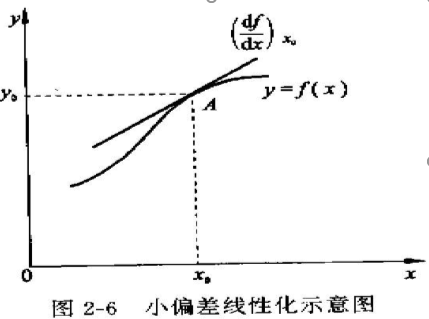
设在平衡状态工作点$A(x_o,y_o)$处连续可微,则
在该点附近用泰勒级数展开
$y = f(x) = f(x_o) + \left( \dfrac{df(x)}{dx} \right)_{x_o}(x - x_o) + \dfrac{1}{2!}\left( \dfrac{d^2f(x)}{dx^2} \right)_{x_o}{(x - x_o)^2} + \cdots $
增量较小时略去其高次幂项,则有
$y - y_o = f(x) - f(x_o) = \left( \dfrac{df(x)}{dx} \right)_{x_o}(x - x_o)$

特别提醒:
⑴上述非线性环节不是指典型的非线性特性(如间隙、库仑干摩擦、饱和特性等),它是可以用泰勒级数展开的。
⑵实际的工作情况在工作点附近。
⑶变量的变化必须是小范围的。其近似程度与工作点附近的非线性情况及变量变化范围有关。
4、线性定常微分方程的求解(拉氏变换法)
常用微分方程的解法
- 直接解析法(分离变量法)
- 适用于少量简单的情况
- Laplace变换解析法
- 仅适用于线性时不变情况
- 状态转移矩阵法
- 仅适用于线性时不变情况
- 数值法
- 适用于所有情况
本节讨论用Laplace变换法解线性时不变微分方程
- 适用于所有情况
拉氏变换法 例2-6
[例2-6]已知$L=1H,C=1F,R=1\text{欧姆}$,且电容上的初始电压$U_0(0)=0.1V$,初始电流$i(0)=0.1A$,电源电压$u_r(t)=1V$。求电路突然接通电源时,电容电压$u_0(t)$的变化规律。
解:
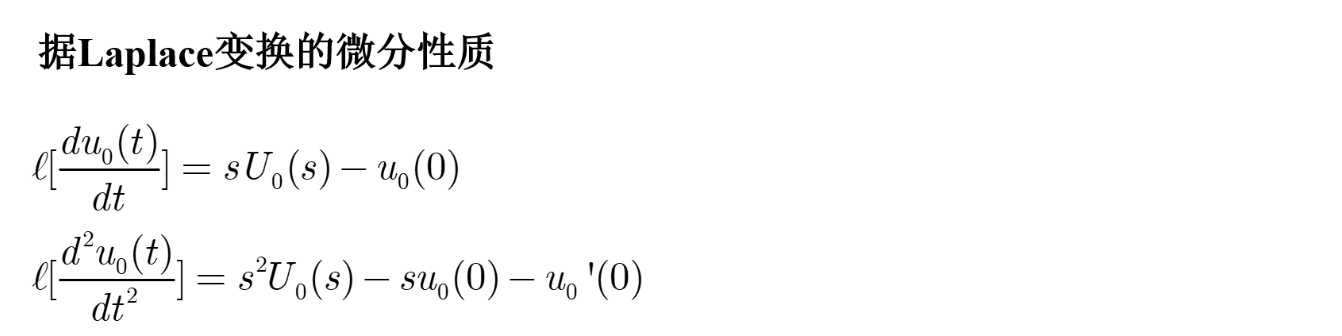


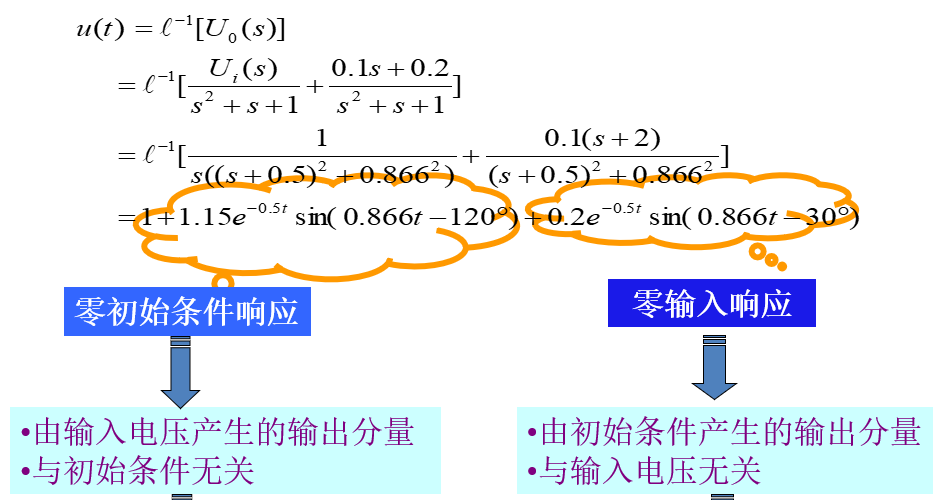

零初始条件响应+零输入响应=单位阶跃响应
Laplace法解线性定常微分方程归纳
- 考虑初始条件,
对微分方程中的每一项分别进行拉氏变换,将微分方程转换为变量s的代数方程; - 由代数方程
求出输出量的拉氏变换表达式,使之成为典型分式之和; 反Laplace变换得到输出量的时域表达式。
5、运动的模态(振型)
齐次微分方程的解:通解+特解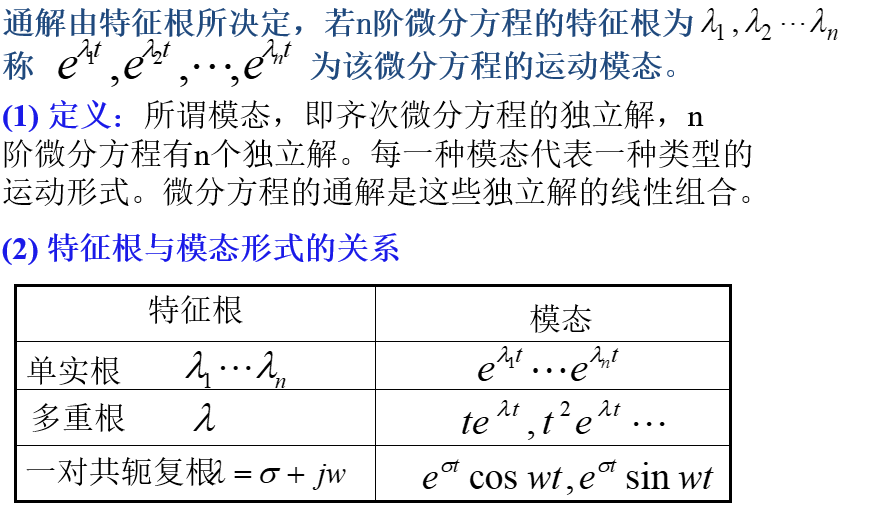
本文链接: 2.1 时域数学模型

