劳斯稳定判据

劳斯稳定判据

应用劳斯判据分析系统的稳定性时，可按下述方法进行。将系统的特征方程写成如下标准形式: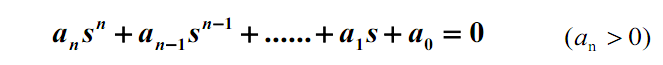

将方程各项系数组成劳斯表: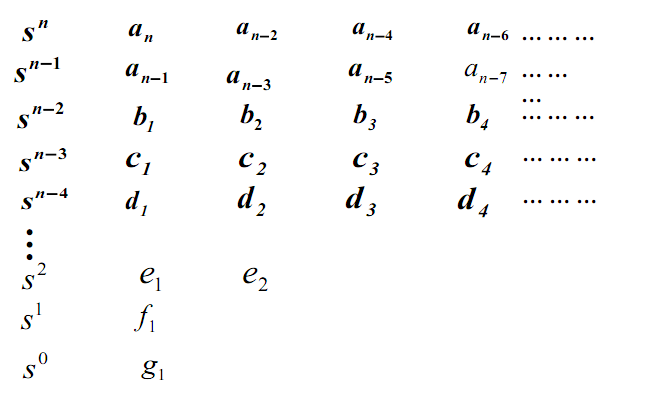

劳斯表中第一行第二行写法固定:

第一行从最高项的系数$a_n$,开始写,然后是第3项的系数,第三列写第5项的系数,依次类推(奇数项)
第二行从第2项的系数$a_{n-1}$开始写,第二列写第4项的系数,第三列写第6项的系数,依次类推(偶数项)

从第三行开始要根据前两行的进行计算得到: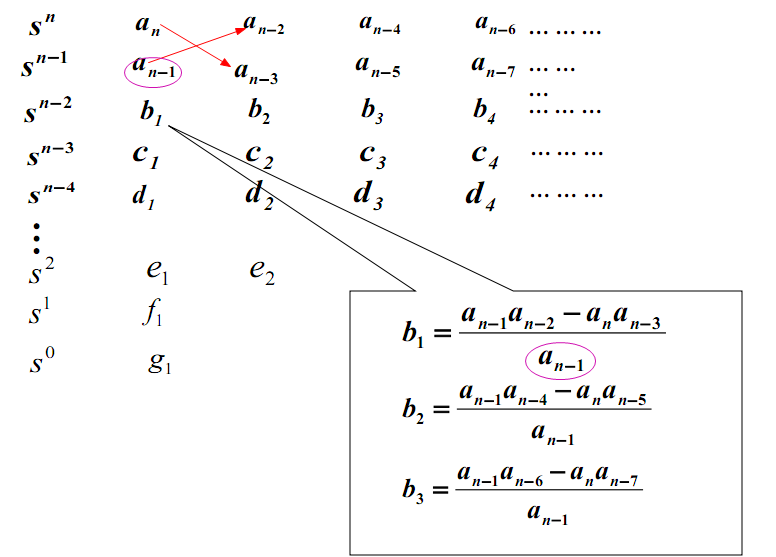

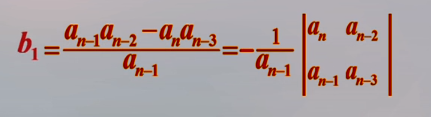
第三行系数的计算一直进行到其余的b值全部等于零为止。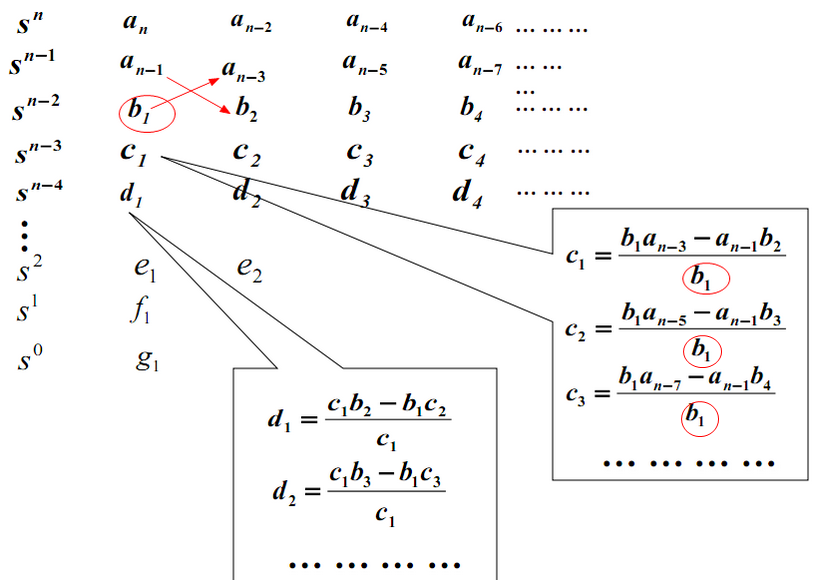

用同样的前两行系数交叉相乘的方法，可以计算$c,d,e,f,g$等各行的系数。这个计算过程一直进行到n+1行为止。
为了简化运算，可以用一个正整数去乘或除某一行的各项,这样并不会改变系统的稳定性.

劳斯表第一列所有系数均不为零的情况

如果劳斯表中第一列的系数都具有相同的符号，则系统是稳定的，否则系统是不稳定的。且不稳定根的个数等于劳斯表中第一列系数符号改变的次数。

例题

已知系统的特征方程为:
$s^5+6s^4+14s^3+17s^2+10s+2=0$
试用劳斯判据分析系统的稳定性。
解:
列出劳斯表如下:


$s^5$	$1$	$14$	$10$
$s^4$	$6$	$17$	$2$
$s^3$	$6\times\dfrac{6\times14-1\times17}{6}=6\times\dfrac{67}{6}=67$	$6\times\dfrac{6\times10-1\times2}{6}=6\times\dfrac{58}{6}=58$	$6\times\dfrac{6\times0-1\times0}{6}=6\times0=0$
$s^2$	$67\times\dfrac{67\times17-6\times58}{67}=791$	$67\times2-6\times0=134$(同乘以67简化计算)
$s^1$	$791\times58-67\times134=36900$
$s^0$	$36900\times134-791\times0 36900=134$

由于第一列系数的符号相同，故系统稳定

例题2

已知系统的特征方程为:
$s^4+2s^3+s^2+s+1=0$
试用劳斯判据判断系统的稳定性。
解：列劳斯表如下:


$s^4$	$1$	$1$	$1$
$s^3$	$2$	$1$	$0$
$s^2$	$2\times\dfrac{2\times1-1\times1}{2}=1$	$2\times\dfrac{2\times1-1\times0}{2}=2$
$s^1$	$\dfrac{1\times1-2\times2}{1}=-3$
$s^0$	$\dfrac{-3\times2-1\times0}{-3}=2$

由于劳斯表第一列的系数变号两次，一次由$1$变为$-3$ ，另一次由$-3$变为$2$，故特征方程有两个根在S平面右半部分，系统是不稳定的。

情况2

劳斯表某行的第一列系数等于零，而其余各项不全为零的情况
当劳斯表某一行的第一列系数为零，而其余项不全为零，可用一个很小的正数$\varepsilon$代替第一列的零项，然后按照通常方法计算劳斯表中的其余项。

临界稳定

如果$\varepsilon$同列上下元素均为正数,表示有一对纯虛根(或零根)存在,系统处于临界稳定。
如果符号相反,则认为有变号,系统不稳定,不稳定根的个数由符号改变的次数决定。

例题

已知系统的开环传递函数如下,试判断系统的稳定性。
$G(s)H(s)=\dfrac{s^2+s+2}{s^4+s^3+s^2+s+3}$
【解】题目给出的是开环传递函数,首先要建立闭环特征方程:
$1+G(s)H(s)=0$
代入闭环传递函数:
$$
\begin{aligned}
1+G(s)H(s)=&1+\dfrac{s^2+s+2}{s^4+s^3+s^2+s+3} \\
=&\dfrac{s^4+s^3+2s^2+2s+5}{s^4+s^3+s^2+s+3} \\
=&0 \\
\end{aligned}
$$
整理后,得到闭环系统的特征方程为:
$s^4+s^3+2s^2+2s+5=0$
然后构建劳斯表


$s^4$	$1$	$2$	$5$
$s^3$	$1$	$2$	$0$
$s^2$	$\dfrac{1\times2-1\times2}{1}=0=\varepsilon$	$\dfrac{1\times5-1\times0}{1}=5$
$s^1$	$\dfrac{\varepsilon\times2-1\times5}{\varepsilon}=\dfrac{2\varepsilon-5}{\varepsilon}$
$s^0$	$\dfrac{\dfrac{2\varepsilon-5}{\varepsilon}\times5-\varepsilon\times0}{\dfrac{2\varepsilon-5}{\varepsilon}}=5$

当$\varepsilon$的取值足够小时，$\dfrac{2\varepsilon-5}{\varepsilon}$将取负值，故劳斯表第一列系数变号两次(负变正,正变负)，由劳斯判据可知，特征方程有两个根具有正实部，系统是不稳定的。

情况3

当劳斯表某行所有元素均为零时。
如果劳斯表中某一行（如第$k$行）各项为零，这说明在$S$平面内存在以原点为对称的特征根。
例如$P=\pm\sigma$，$P=\pm j\omega$，$P=\pm\sigma\pm j\omega$等等。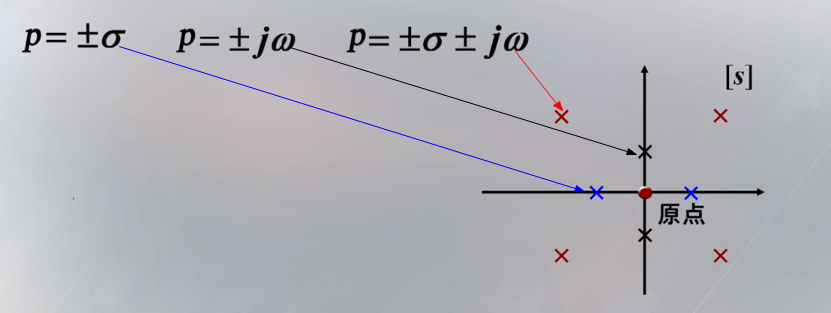

显然，系统是不稳定的。

确定特征跟的分别情况

此时，为了确定根的分布情况，
可按下列步骤处理：

利用第k-1行的系数构成辅助方程。通常来说,辅助方程关于$s$的次数总是偶次的;
求辅助方程对s的导数，将其系数代替原全部为零的k行，继续计算劳斯表.
特征方程中以原点为对称的根可由辅助方程求得。

总结

特征方程系数全部为正数
当满足特征方程系数全部为正数时,劳斯表的第一列都大于零时,系统是稳定的。如果第一列出现小于零的系数,则系统是不稳定的。
若计算劳斯表时出现情况2和情况3,此时系统临界稳定或者不稳定.此时为确定系统极点的分布情况,可按情况(2)和(3)的方法处理。

例题给出结构体判断系统是否稳定

已知系统的结构图如图所示。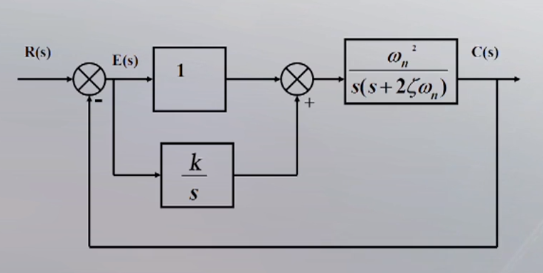

当$\zeta=0.2,\omega_n=86.6$时试确定$k$为何值时,系统稳定
解:

将反馈的输出通路断开,反馈信号对于参考输入信号的传递函数称为开环传递函数(反馈除以输入)。这时前向通路传递函数与反馈通路传递函数的乘积为该系统的开环传递函数。

前向通路传递函数为:
$(1+\dfrac{k}{s})\dfrac{\omega_n^2}{s(s+2\zeta\omega_n)}$
反馈通路传递函数为:$1$
所以开环传递函数:
$$
\begin{aligned}
G(s)H(s)=&(1+\dfrac{k}{s})\dfrac{\omega_n^2}{s(s+2\zeta\omega_n)} \\
=&(\dfrac{s+k}{s})\dfrac{\omega_n^2}{s(s+2\zeta\omega_n)} \\
=&\dfrac{(s+k)\omega_n^2}{s^2(s+2\zeta\omega_n)} \\
\end{aligned}
$$
闭环传递函数为:
$$
\begin{aligned}
\varPhi(s)=&\dfrac{G(s)}{1+G(s)H(s)} \\
=&\dfrac{\dfrac{(s+k)\omega_n^2}{s^2(s+2\zeta\omega_n)}}{1+\dfrac{(s+k)\omega_n^2}{s^2(s+2\zeta\omega_n)}} \\
=&\dfrac{(s+k)\omega_n^2}{s^3+2s^2\zeta\omega_n+s\omega_n^2+k\omega_n^2} \\
\end{aligned}
$$
得到闭环传递函数,令闭环传递函数的分母为0,则可以得到闭环特征方程为:
$s^3+2s^2\zeta\omega_n+s\omega_n^2+k\omega_n^2=0$
将$\zeta=0.2,\omega_n=86.6$代入特征方程得：
$s^3+2s^2\times0.2\times86.6+s\times86.6^2+k86.6^2=0$
$s^3+34.64s^2+7499.56s+7499.56k=0$,四舍五入得到:
$s^3+34.6s^2+7500s+7500k=0$
列出劳斯表,要使系统稳定,劳斯表第一列所有元素必须全为正数，可以列出关于$k$的方程,从而求出$k$的取值范围