2-11
2-11在图2-51中,已知$G(s)$和$H(s)$两方框相对应的微分方程分别是:
$
6\dfrac{dc(t)}{dt}+10c(t)=20e(t)
$,$
20\dfrac{db(t)}{dt}+5b(t)=10c(t)
$
且初始条件均为零,试求传递函数$C(s)/R(s)$及$E(s)/R(s)$.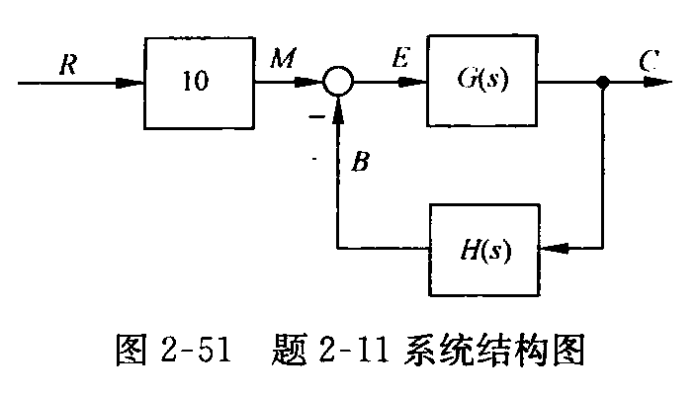
知识点窍:传递函数、拉氏变换
逻辑推理:由系统的微分方程通过拉氏变换得出系统的传递函数。
$L[\dfrac{d}{dt}f(t)]=sF(s)-f(0)$
解题过程:对题目所给微分方程两边同时作拉氏变换,
$
\begin{cases}
6[sC(s)-c(0)]+10C(s)=20E(s) \\
20[sB(s)-b(0)]+5B(s)=10C(s)
\end{cases}
$
由于已知初始条件均为0,所以有:$
\begin{cases}
c(0)=0 \\
b(0)=0
\end{cases}
$,代入上面的式子得到:
$
\begin{cases}
6sC(s)+10C(s)=20E(s) \\
20sB(s)+5B(s)=10C(s)
\end{cases}
$
从图可以看出:
$
\begin{cases}
G(s)=\dfrac{C(s)}{E(s)}\\
H(s)=\dfrac{B(s)}{C(s)}
\end{cases}
$
解方程得到:
$
\begin{cases}
G(s)=\dfrac{C(s)}{E(s)}=\dfrac{20}{6s+10}=\dfrac{10}{3s+5}\\
H(s)=\dfrac{B(s)}{C(s)}=\dfrac{10}{20s+5}=\dfrac{2}{4s+1}
\end{cases}
$
等效框图如下: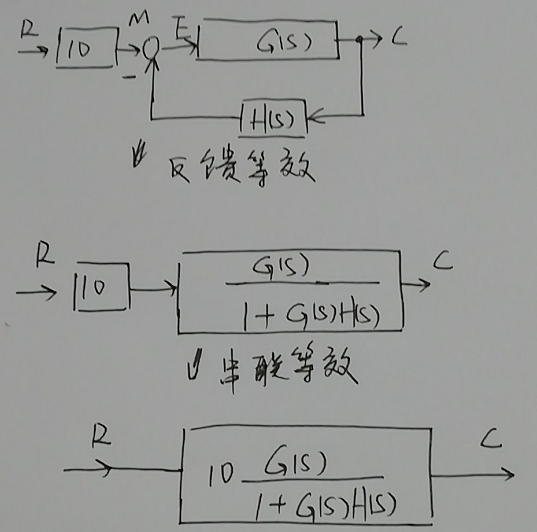
又由图可看出:$R(s)\times 10\times \dfrac{G(s)}{1+G(s)H(s)}=C(s)$
所以$\dfrac{C(s)}{R(s)}=\dfrac{10G(s)}{1+G(s)H(s)}$,
代入$\begin{cases} G(s)=\dfrac{C(s)}{E(s)}=\dfrac{10}{3s+5}\\ H(s)=\dfrac{B(s)}{C(s)}=\dfrac{2}{4s+1} \end{cases}$
可得到:
$$
\begin{aligned}
\dfrac{C(s)}{R(s)}=&\dfrac{10G(s)}{1+G(s)H(s)} \\
=&\dfrac{10\times\dfrac{10}{3s+5}}{1+\dfrac{10}{3s+5}\dfrac{2}{4s+1}} \\
=&\dfrac{10\times10(4s+1)}{(3s+5)(4s+1)+10\times2} \\
=&\dfrac{100(4s+1)}{(3s+5)(4s+1)+10\times2} \\
=&\dfrac{100(4s+1)}{12s^2+23s+5+20} \\
=&\dfrac{100(4s+1)}{12s^2+23s+25} \\
\end{aligned}
$$
由图可知$E(s)=M(s)-B(s)=10R(s)-C(s)H(s)=[10-\dfrac{C(s)}{R(s)}H(s)]R(s)$,
所以$\dfrac{E(s)}{R(s)}=10-\dfrac{C(s)}{R(s)}H(s)=10-\dfrac{100(4s+1)}{12s^2+23s+25}\dfrac{2}{4s+1}$
整理得到:
$$
\begin{aligned}
\dfrac{E(s)}{R(s)}=&10-\dfrac{100(4s+1)}{12s^2+23s+25}\dfrac{2}{4s+1} \\
=&10-\dfrac{100\times2}{12s^2+23s+25} \\
=&10-\dfrac{200}{12s^2+23s+25} \\
=&\dfrac{10(12s^2+23s+25)-200}{12s^2+23s+25} \\
=&\dfrac{10(12s^2+23s+5)}{12s^2+23s+25} \\
\end{aligned}
$$
答案
$$
\begin{cases}
\dfrac{C(s)}{R(s)}=\dfrac{100(4s+1)}{12s^2+23s+25} \\
\dfrac{E(s)}{R(s)}=\dfrac{10(12s^2+23s+5)}{12s^2+23s+25}
\end{cases}
$$
原文链接: 自动控制原理 作业题 2-11

