引言
一、信号流图的组成和性质
二、信号流图的绘制
三、梅森公式
四、闭环系统的传递函数
一、信号流图的组成及性质
(1) 起源
梅森利用图示法描述一个或一组线性代数方程式, 由[节点]和[支路]组成的一种信号传递网络。
(2) 基本单元
a) 节点:代表变量,用小圆圈表示。
B)支路:代表因果关系的乘法因子,表示两个变量之间的传递方向及增益,用单向线段表示。
(3) 基本性质
- 节点代表变量。
- 每个节点变量等于所有流入该节点的信号之代数和。
- 从该节点流出的信号都等于该节点变量。
- 支路代表因果关系的乘法因子。相当于乘法器,信号流经支路时,被乘以支路增益而变换为另一信号。
- 在支路上信号传递是单向的。
- 信号流图不是唯一的。
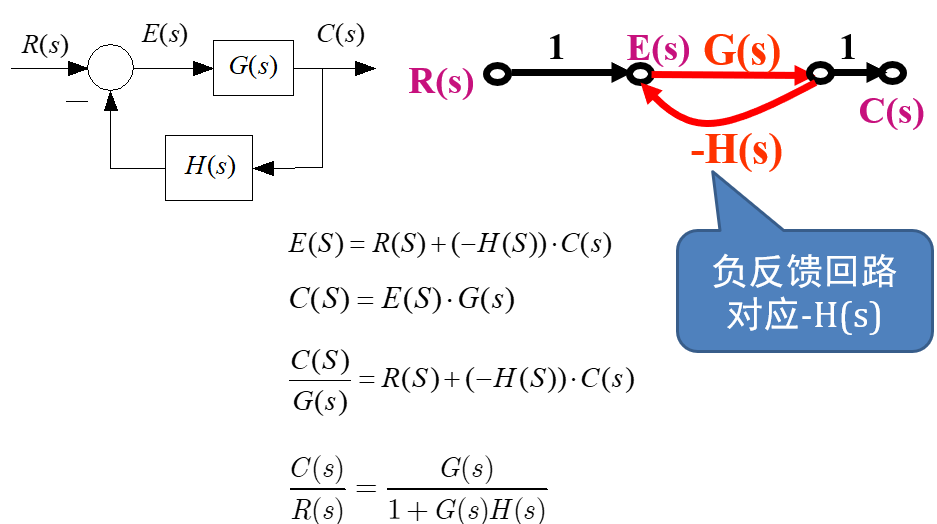
(4) 典型信号流图
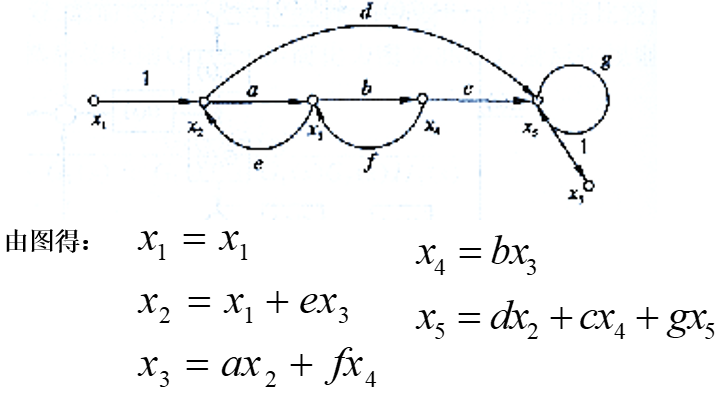
(5) 常用术语
源节点(输入节点):只有信号输出支路,没有信号输入支路
阱节点(输出节点):只有信号输入支路,没有信号输出支路
混合节点:既有信号输出支路,又有信号输入支路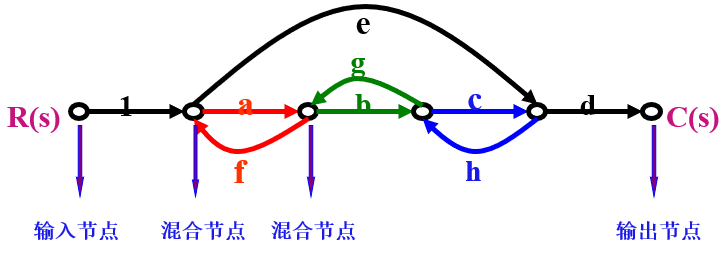
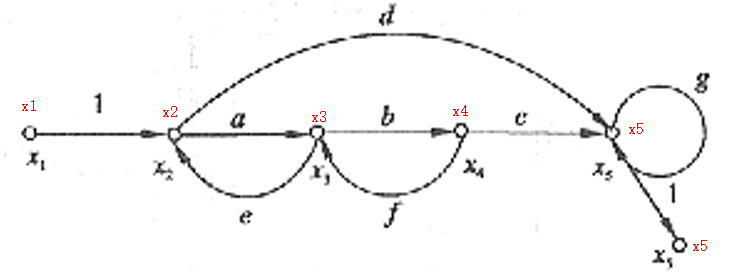
前向通路:信号从输入节点到输出节点传递时,每个节点只通过一次的通路。前向通路上个支路增益的乘积称为前向通路总增益
- 前向通路$x_1 \to x_2 \to x_3 \to x_4 \to x_5$,前向通路增益$p_1 = abc$
- 前向通路$x_1\to x_2\to x_5$,前向通路增益$p_2 = d$
回路(单独回路):起点和终点在同一节点,而且信号通过每个节点不多于一次的闭合通路
- 回路1$x_2 \to x_3 \to x_2$,回路1增益$l_1= ae$
- 回路2$x_3\tox_4 \to x_3$,回路2增益$$l_2 = bf$
- 回路3$x_5 \to x_5$,回路3增益$l_3= g$
不接触回路:回路之间没有公共节点
- 回路1和回路3
- 回路2和回路3
回路(单独回路):起点和终点在同一节点,而且信号通过每个节点不多于一次的闭合通路
二、信号流图的绘制
1、由系统微分方程绘制信号流图:先取拉氏变换,再绘制。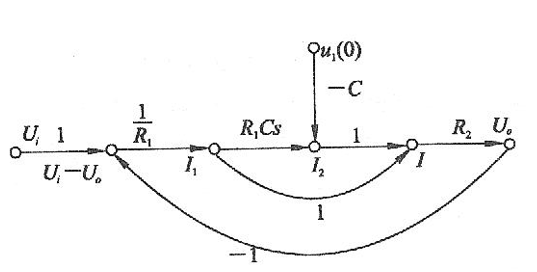
1.结构图的输入处加输入节点, 标“输入变量名”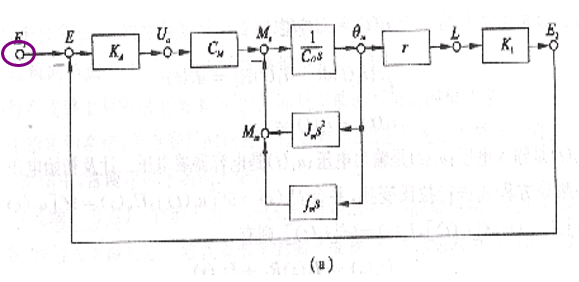
2.方框间的连接线中应加信号节点,标“线输变量名”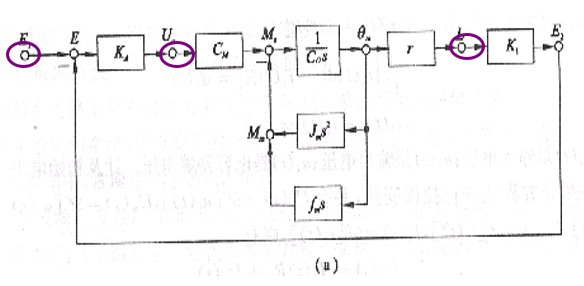
3.连线分流处应加信号节点, 标“线输变量名”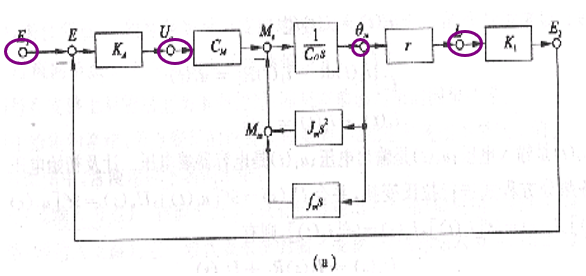
4.比较点处应在比较点的信号流出处标加信号节点,标“比较点输出变量名”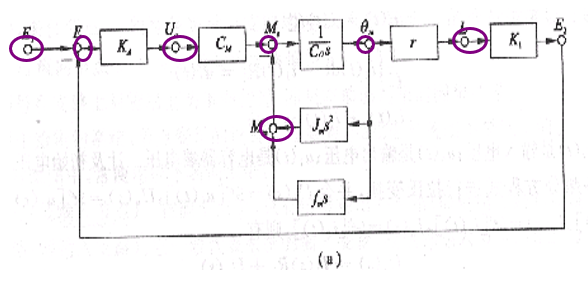
5.结构图的输出处加输出节点,标“输出变量名”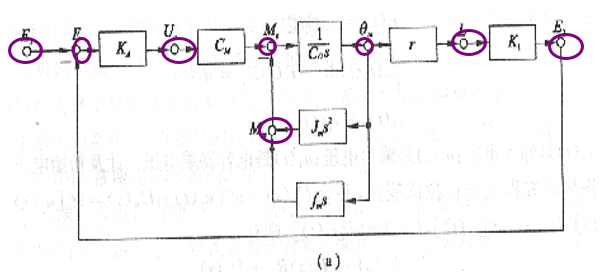
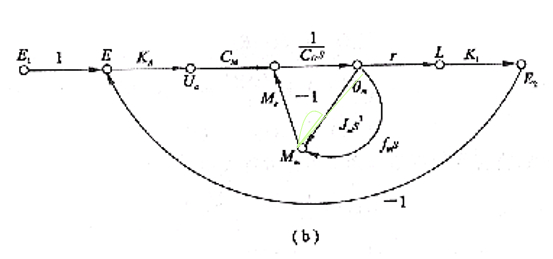
3、比较点和节点对应关系
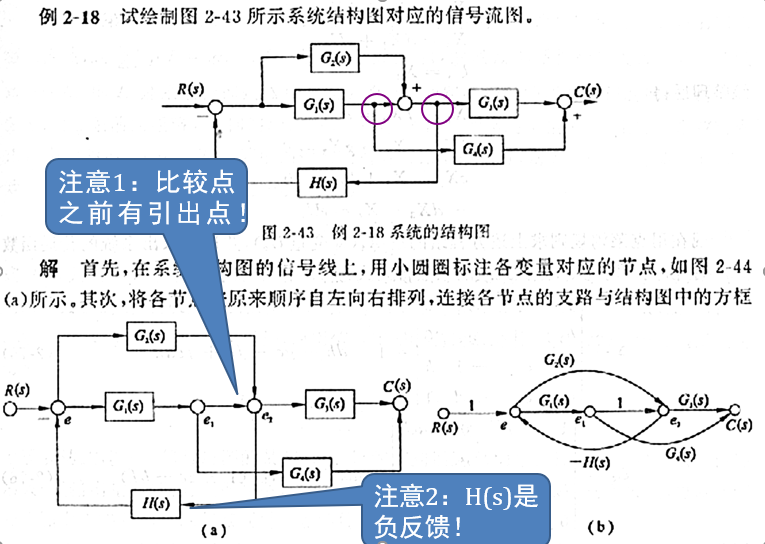
(1) 在结构图比较点之前没有引出点(比较点之后可以有引出点),只需在比较点后设置一个节点便可,如(a)
(2) 在比较点之前有引出点事,就需在引出点和比较点各设置一个节点,分别标志两个变量,它们之间的支路增益为1,如(b)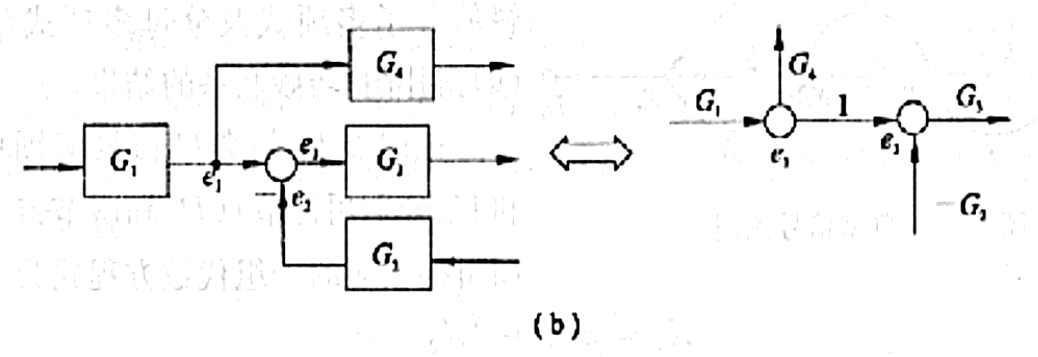
例题
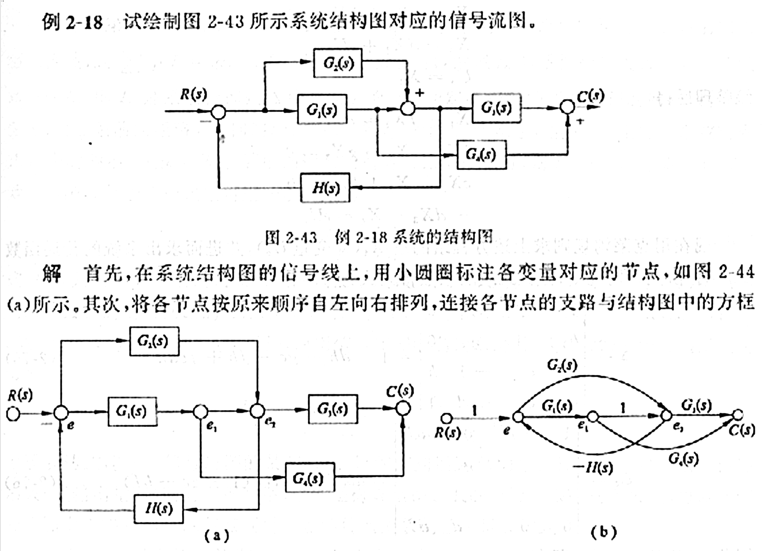
三、梅森公式的推导
已知信号流图如图所示,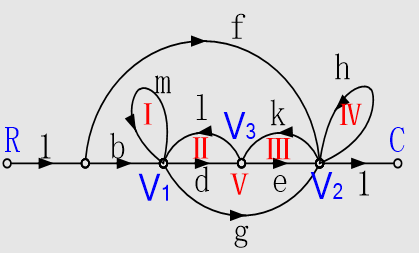
所对应的代数方程为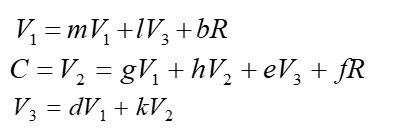
$$
\begin{aligned}
(1-m)V_1&+&0V_2&+&lV_3=&bR \nonumber \\
-gV_1&+&(1-h)V_2&-&eV_3=&fR \nonumber \\
-dV_1&-&kV2&+&V_3=&0R \nonumber \\
\end{aligned}
$$
以R为输入,$V_2$为输出则可整理成下列方程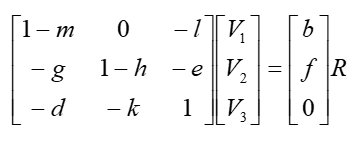

本文链接: 2-3 信号流图

