隐函数的导数
显函数

隐函数


隐函数的显化

例1

求隐函数导数的方法

例2


对数求导法

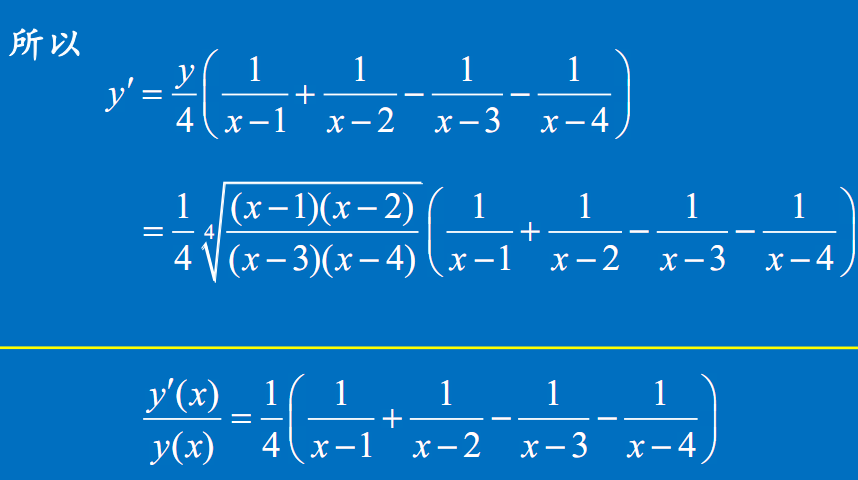

对数求导法就是先在$y=f(x)$的两边取对数,然后求出y的导数
例3
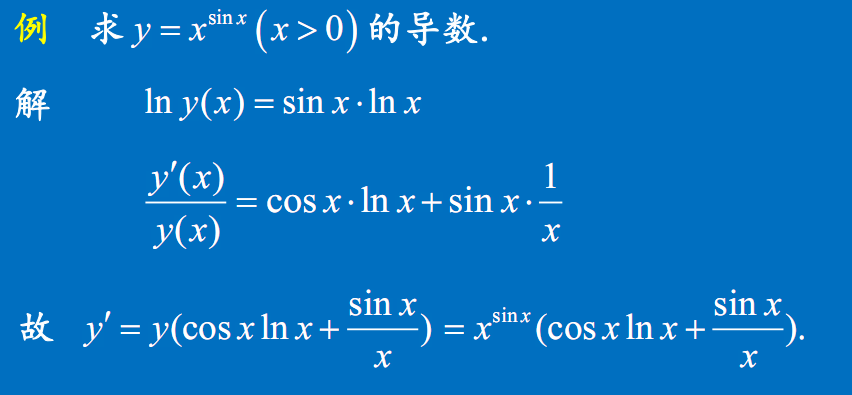
$(\ln y(x))’=(\sin x \ln x)$
$\dfrac{1}{y(x)}y’(x)=\cos x\ln x+\sin x \dfrac{1}{x}$
$$
\begin{aligned}
y’=&y(\cos x\ln x+\sin x \dfrac{1}{x}) \nonumber \\
=&x^{\sin x}(\cos x\ln x+\sin x \dfrac{1}{x}) \nonumber \\
\end{aligned}
$$
另一方法
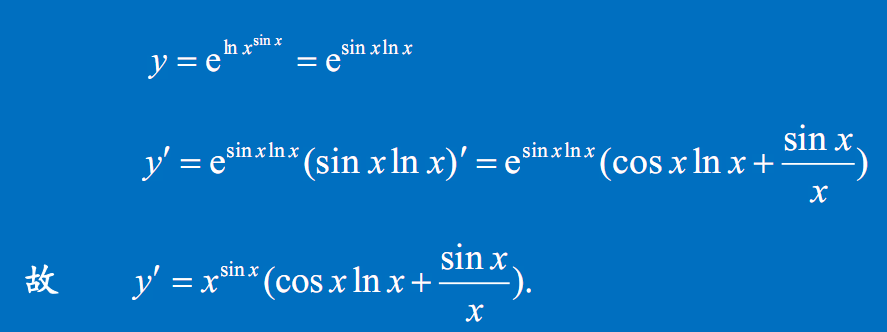
由参数方程所确定的函数的导数
由参数方程所确定的函数


求导方法


$
\begin{cases}
x=\varphi(t) \\
y=\psi(t)
\end{cases}
$,$t=\varphi^{-1}(x)$
$\dfrac{dy}{dx}=\dfrac{dy}{dt}\cdot \dfrac{dt}{dx}=\dfrac{dy}{dx}\cdot \dfrac{1}{\dfrac{dx}{dt}}= \dfrac{\psi’(t)}{\varphi’(t)}$,即:
$\dfrac{dy}{dx}=\dfrac{\psi’(t)}{\varphi’(t)}$或:
$\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}$
例题

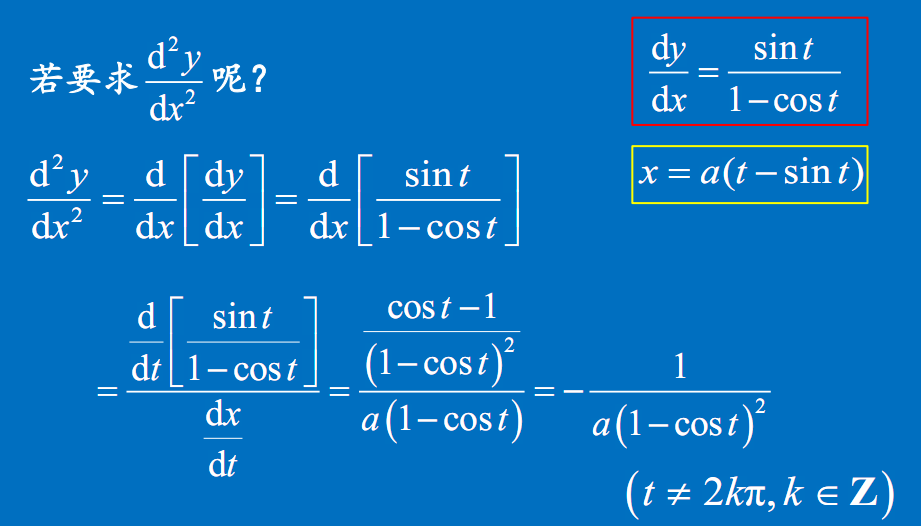
参数方程的二阶导数
二阶导数不能直接由参数方程求出

方法
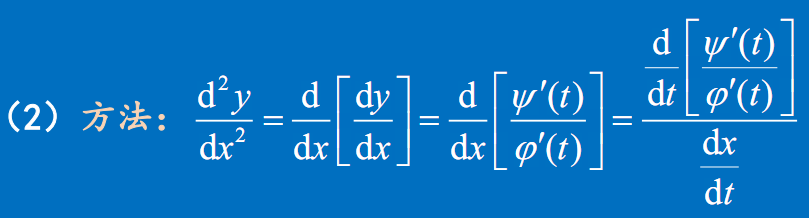
公式
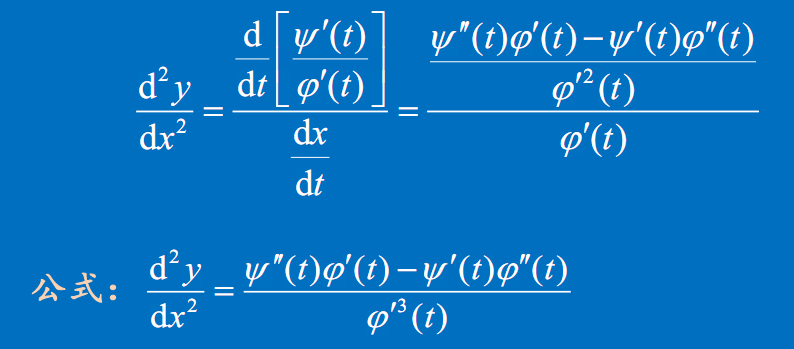
$\dfrac{d^2y}{dx^2}=\dfrac{\psi’’(t)\varphi’(t)-\psi’(t)\psi’’(t)}{\varphi’^3(t)}$
问题
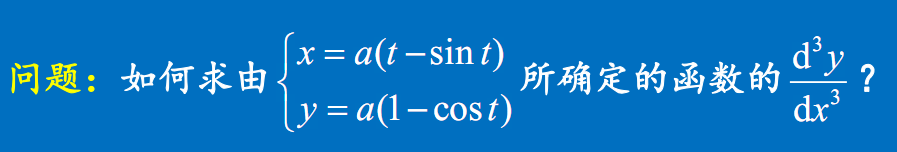
习题
题1

解:
$x=0$代入原方程:
$$
\begin{aligned}
y-e^{2\times 0 \times y}=&1 \nonumber \\
y-1=&1 \nonumber \\
\end{aligned}
$$
解得:$y=2$
方程两本同时对x求导:
$$
\begin{aligned}
\dfrac{d}{dx}(y-e^{2xy})=&\dfrac{d}{dx}1 \nonumber \\
\dfrac{dy}{dx}-e^{2xy}\dfrac{d}{dx}(2xy)=&0 \nonumber \\
\dfrac{dy}{dx}-e^{2xy}(2y+2x\dfrac{dy}{dx})=&0 \nonumber \\
\dfrac{dy}{dx}-e^{2xy}2x\dfrac{dy}{dx}=&e^{2xy}2y \nonumber \\
(1-e^{2xy}2x)\dfrac{dy}{dx}=&e^{2xy}2y \nonumber \\
\dfrac{dy}{dx}=&\dfrac{e^{2xy}2y}{1-e^{2xy}2x} \nonumber \\
\end{aligned}
$$
$\left. \dfrac{dy}{dx}\right|_{x=0}=\dfrac{e^{2\times 0\times y}2y}{1-e^{2\times 0\times y}2\times 0}
=2y=4$
题2

解:
$\varphi’(t)=\dfrac{dx}{dt}=3e^{-t}\times -1=-3e^{-t}$
$\varphi’’(t)=\dfrac{d^2x}{dt^2}=3e^{-t}$
$\psi’(t)=\dfrac{dy}{dt}=2e^{t}\times 1=2e^{t}$
$\psi’’(t)=\dfrac{d^2y}{dt^2}=2e^{t}\times 1=2e^{t}$
$\dfrac{d^2y}{dx^2}=\dfrac{\psi’’(t)\varphi’(t)-\psi’(t)\psi’’(t)}{\varphi’^3(t)}
=\dfrac{2e^{t}\times -3e^{-t}-(2e^{t}\times 3e^{-t})}{(-3e^{-t})^3}
=\dfrac{-4e^{t}3e^{-t}}{-3^3(e^{-t})^3}
=\dfrac{4e^{t}}{3^2(e^{-t})^2}
=\dfrac{4e^{t}}{9e^{-2t}}
=\dfrac{4e^{3t}}{9}
$
题3

解:方程两边同时对x求导得:
$$
\begin{aligned}
2yy’-2y-2xy’=&0 \nonumber \\
(2y-2x)y’=&2y \nonumber \\
y’=&\dfrac{2y}{2y-2x} \nonumber \\
y’=&\dfrac{y}{y-x} \nonumber \\
\end{aligned}
$$
题4

解:方程两边同时都x求导得到:
$cosy-xy’siny+e^yy’=0\\
y’(e^y-xsiny)=-cosy\\
y’=\dfrac{-cosy}{(e^y-xsiny)}
$
$\left. y’\right|_{x=0,y=0 }=\dfrac{-cos0}{e^0-0sin0}=\dfrac{-1}{1-0}=-1$
则切线方程为:
$$
\begin{aligned}
y-0=&-1(x-0) \nonumber \\
y=&-x \nonumber \\
\end{aligned}
$$
题5

$\dfrac{dy}{dt}=3bt^2$
$\dfrac{dx}{dt}=2at$
$\dfrac{dy}{dx}=\dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}}=\dfrac{3bt^2}{2at}=\dfrac{3bt}{2a}$
本文链接: 2-4隐函数及由参方程所确定的函数的导数

