自变量趋于有限值时函数的极限
设$f(x)$在点x的某个去心邻域内有定义如果在$x \rightarrow x_0$的过程中,对应的函数值$f(x)$无限接近于确定的数值A,则称A为$f(x)$当$x \rightarrow x_0$时的极限
极限定义

几何意义
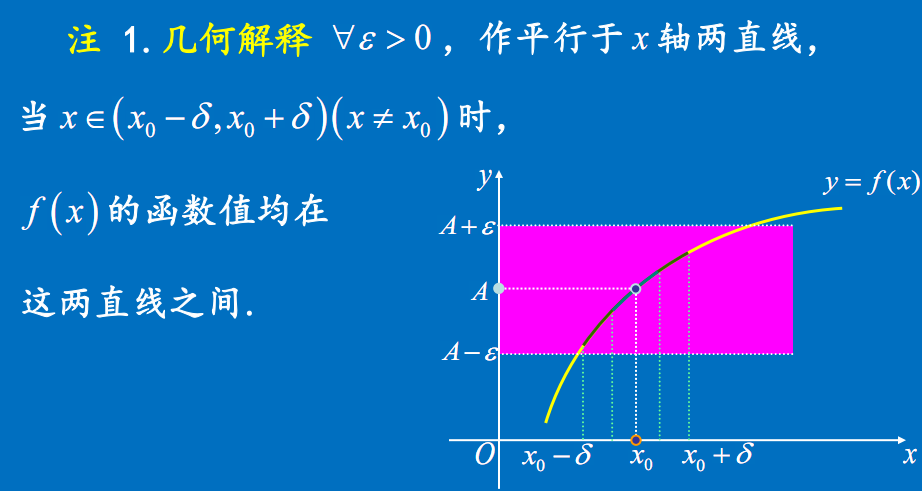
极限与函数在该点是否有定义无关
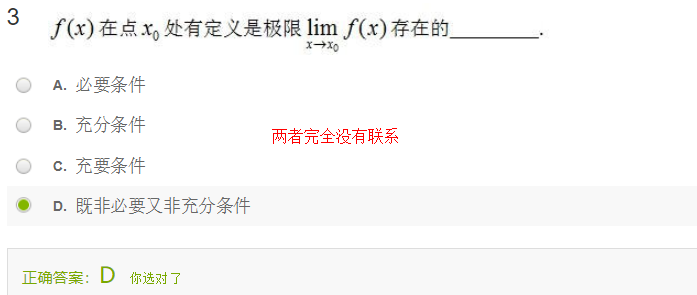
2.$x \rightarrow x_0$时函数$f(x)$有没有极限与$f(x)$在$x=x_0$处是否有定义无关;
常见函数的极限
常数函数C的极限是常数C
$\lim \limits_{x \to x_0}C=C$
正比例函数x的极限是x_0
$\lim \limits_{x \to x_0}x=x_0$
$\lim \limits_{x \to 1}(4x-1)=3$
$\lim \limits_{x \to 1}\dfrac{x^2-1}{x-1}=2$
左右极限
$\lim \limits_{x \to x_0}f(x)=A$中“$x \to x_0$”的实质含义:x既从x的左侧也从x的右侧趋于$x_0$
右极限

左极限

右极限和左极限统称为单侧极限
定理

例题

习题



自变量趋于无穷大时扬数的极限
描述性定义

数学定义

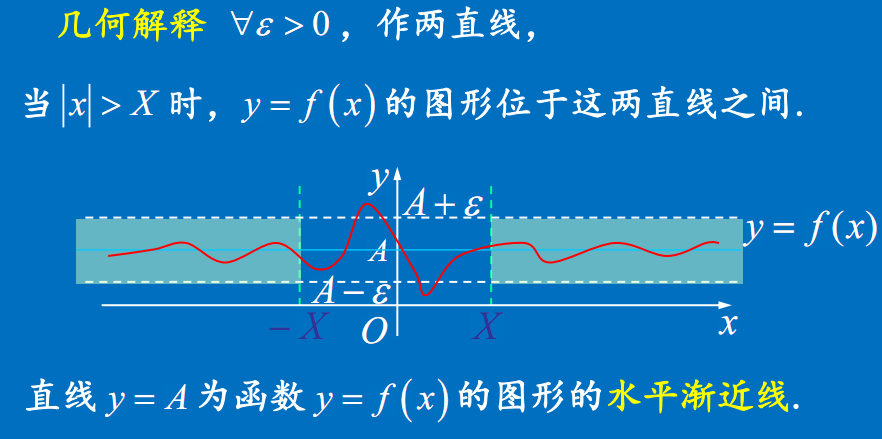
几何解释
水平渐近线
左右极限

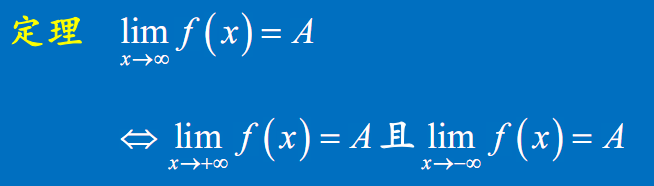
例题
证明$\lim \limits_{x \to \infty}\dfrac{1}{x}=0$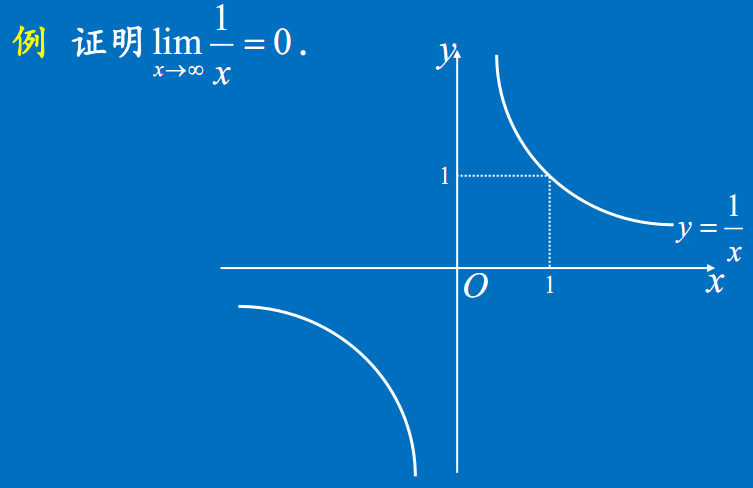

函数极限的性质
以“$limf(x)$”这种形式为代表给出关于函数极限性质的一些定理
定理1(函数极限的唯一性)

定理2(函数极限的局部有界性)

定理3(函数极限的局部保号性)

推论 函数值的绝对值大于极限的绝对值的一半

定理3.5(函数极限的保不等式性)
函数值大的极限也大
推论
极限A比B小则函数f(a)也小于等于f(b)
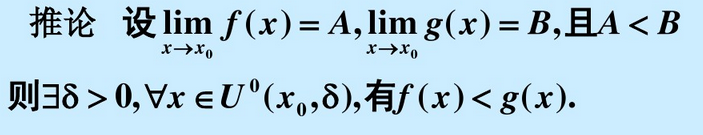
函数值大于等于0则极限也大于等于0

定理4(函数极限与数列极限的关系)

求极限方法举例
多项式与分式函数代入法求极限
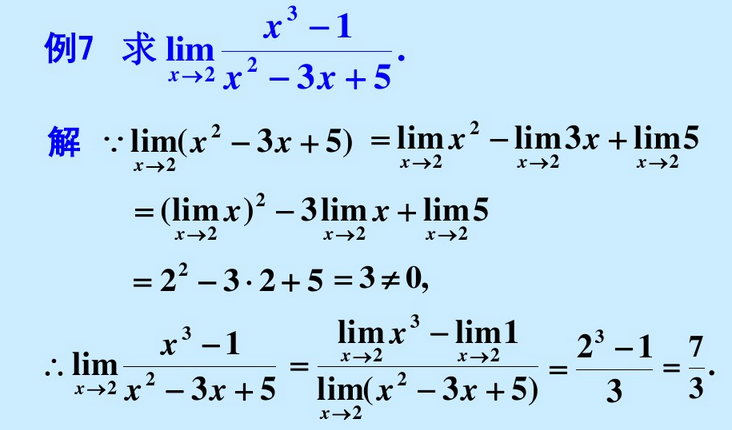

利用无穷大于无穷小的关系求极限

0比0型 消去零因子法

无穷比无穷型 无穷小因子分出法


先变型再求极限

复合函数极限
复合函数极限运算法则–变量代换法则
习题
题1

题2

题3

题4

解:先通分,变型。
$$
\begin{align}
&\lim \limits_{x \to \infty }(\dfrac{x^3}{x^2+1}-\dfrac{x^2}{x-1}) \nonumber \\
=&\lim \limits_{x \to \infty }\dfrac{(x^3)(x-1)-(x^2)(x^2+1)}{(x^2+1)(x-1)} \nonumber \\
=&\lim \limits_{x \to \infty }\dfrac{x^4-x^3-x^4-x^2}{x^3 -x^2+x -1} \nonumber \\
=&\lim \limits_{x \to \infty }\dfrac{-x^3-x^2}{x^3 -x^2+x -1} \nonumber \\
=&-1 \nonumber \\
\end{align}
$$
题5

渐近线,就是区域无穷大时的极限。
参考资料
https://wenku.baidu.com/view/7c9dfdba050876323112129b.html?from=search
本文链接: 1-3函数极限

