连续函数的四则运算的连续性

定理

定理若函数$f(x)$,$g(x)$都在点$x_0$处连续,则$f(x)±g(x)$,$f(x)\cdot g(x)$,$\dfrac{f(x)}{g(x)}(g(x_0)\ne 0)$在点$x_0$处也连续。

反函数连续性

定理

例子

复合函数的连续性

定理

复合函数连续定理

例子

初等函数的连续性

基本初等函数连续定理

基本初等函数在其定义域内是连续的

初等函数连续定理

一切初等函数在其定义区间内都是连续的

注

1.定义区间就是指:包含在定义域内的区间
2.若函数$f(x)$在$x=x_0$处连续,则有$\lim \limits_{x \to x_0}f(x)=f(x_0)$,因此,若$f(x)$是初等函数,且$x_0$是定义区间内的点,此时若求$\lim \limits_{x \to x_0}f(x)$则需求出函数值$f(x_0)$比如:

$\lim \limits_{x \to 0} \sqrt{1-x^2}=\sqrt{1-0^2}=1$

根据连续性求极限

例1

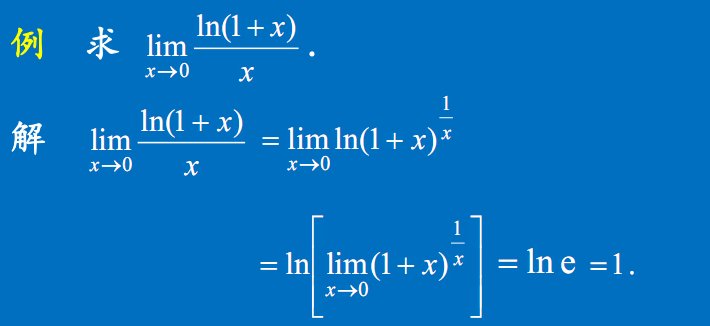
例2

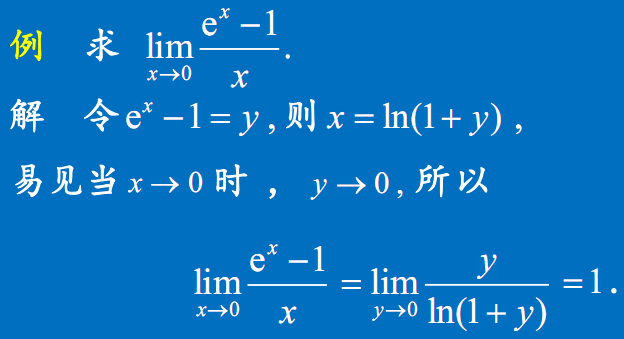
例3

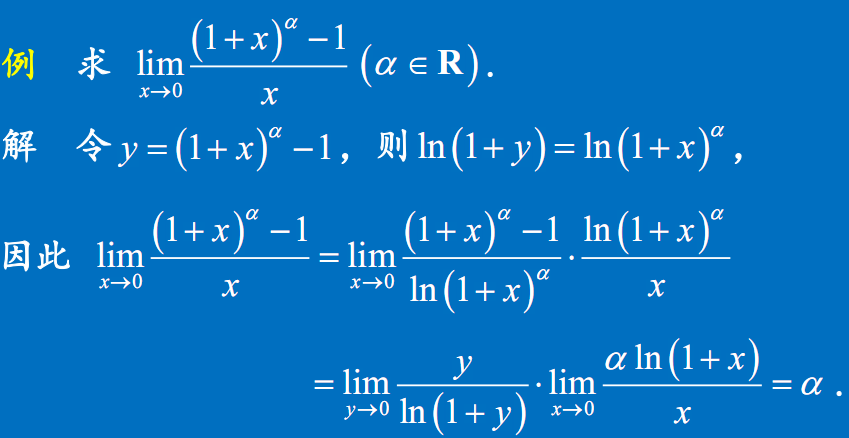
新的等价无穷小关系

由上面的例子可得三个常用的等价无穷小关系式:
当$x \to 0$时，

$ln(1+x) \sim x$
$e^x-1 \sim x$
$(1+x)^\alpha \sim \alpha x$

幂指函数极限求法

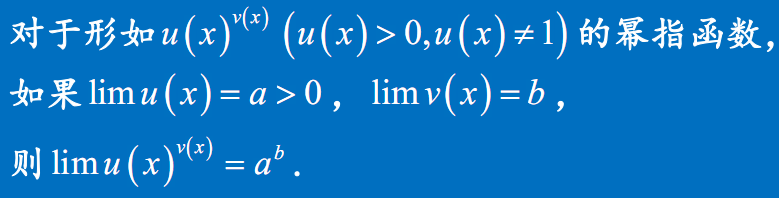
如果底数和指数的极限同时存在则幂指函数的极限等于底数和指数的各自的极限
例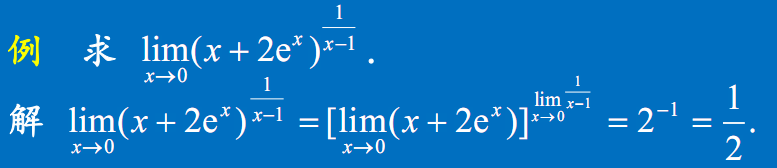

习题

习题1

解:因为 $y=\sqrt{x}$是基本初等函数，$y=\sqrt{x-4}$，$y=\sqrt{5-x}$是初等函数，初等函数在定义区间内连续，所以只需要求出定义区间即可。
$
\begin{cases}
x-4\ge 0 \\
5-x \ge 0
\end{cases}
$ 解得 $
\begin{cases}
x \ge 4 \\
x \le 5
\end{cases}
$
所以连续区间为$[4,5]$

习题2

解:因为连续，所以$\lim \limits_{x \to 0}f(x)=f(0)$,$f(0)=ae^0=a$,
$\lim \limits_{x \to 0}\dfrac{ \sqrt{2-2cosx}}{x}
=\lim \limits_{x \to 0}\dfrac{ \sqrt{2(1-cosx)}}{x}
$
因为$x \to 0$
由等价无穷小公式:

$(1+x)^\alpha \sim \alpha x$,
$1-cosx \sim \dfrac{1}{2}x^2$

所以$
\lim \limits_{x \to 0^-}\dfrac{ \sqrt{2(1-cosx)}}{x}
=\lim \limits_{x \to 0^-}\dfrac{ \sqrt{2\dfrac{1}{2}x^2}}{x}
=\lim \limits_{x \to 0^-}\dfrac{\left|x \right|}{x}
=\dfrac{-x}{x}
=-1
$
注意，$\sqrt{x^2}=\left| x \right|$.

习题3

解:因为连续，$
f(0)=\dfrac{1}{2}0+cos\dfrac{\pi}{2}0
=0+cos0
=1
$，
$
f(1)=\dfrac{1}{2}1+cos\dfrac{\pi}{2}1
=\dfrac{1}{2}+cos\dfrac{\pi}{2}
=\dfrac{1}{2}+0
=\dfrac{1}{2}$

$
\lim \limits_{x \to 0} f(x)
=\lim \limits_{x \to 0} \dfrac{sinax}{x}
=\lim \limits_{x \to 0}\dfrac{ax}{x}
=a
=f(0)
=1
$
$\lim \limits_{x \to 1}f(x)
=\lim \limits_{x \to 1}\dfrac { \sqrt{x} -b}{x-1}
$
令$u(x)=x-1$,则$x=u(x)+1$,$x \to 1$时，$u(x) \to 0$

等价无穷小公式:$\sqrt[n]{1+x}-1 \sim \dfrac{1}{n}x$

$$
\begin{align}
&\lim \limits_{x \to 1}\dfrac { \sqrt{x} -b}{x-1} \nonumber \\
=&\lim \limits_{u(x) \to 0}\dfrac{ \sqrt{1+u(x)} -b}{u(x)} \nonumber \\
=&f(1) \nonumber \\
=&\dfrac{1}{2} \nonumber \\
\end{align}
$$
只有当$b=1$时,
$\lim \limits_{u(x) \to 0}\dfrac{ \sqrt{1+u(x)} -b}{u(x)}
=\lim \limits_{u(x) \to 0}\dfrac{ \sqrt{1+u(x)} -1}{u(x)}
=\lim \limits_{u(x) \to 0}\dfrac{\dfrac{1}{2}x}{x}
=\dfrac{1}{2}
$
所以$(a,b)=(1,1)$