极限的四则运算法则
定理
- 有限个无穷小的和是无穷小
- 有界函数与无穷小的乘积是无穷小
- 注:这里函数的有界性只要求在无穷小的自变量变化范围内成立
实例

推论
- 常数与无穷小的乘积是无穷小
- 有限个无穷小的乘积是无穷小
注无穷小的和、差,积仍是无穷小
定理 极限的四则运算法则
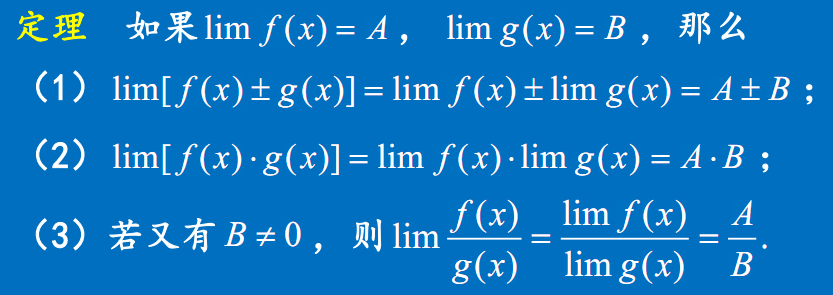
注1.此定理就是极限的四则运算法则,也即函数的和、差、积、商(B≠0)的极限等于函数极限的和、差、积、商.
推论 常数C 乘方n 可以移到极限符号之外
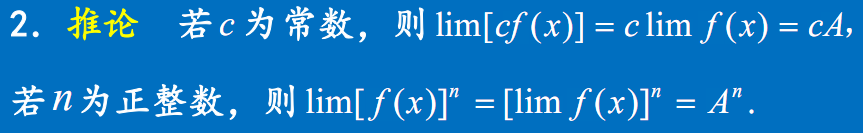
定理 数列极限四则运算

和式的极限
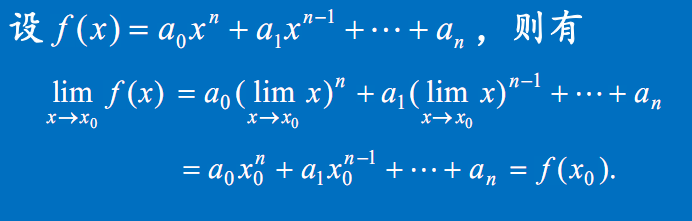
实例
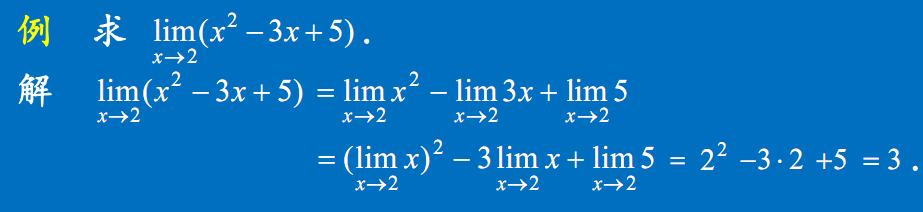
多项式分式的极限

实例
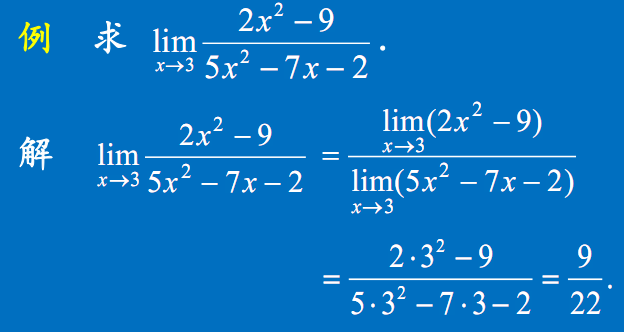
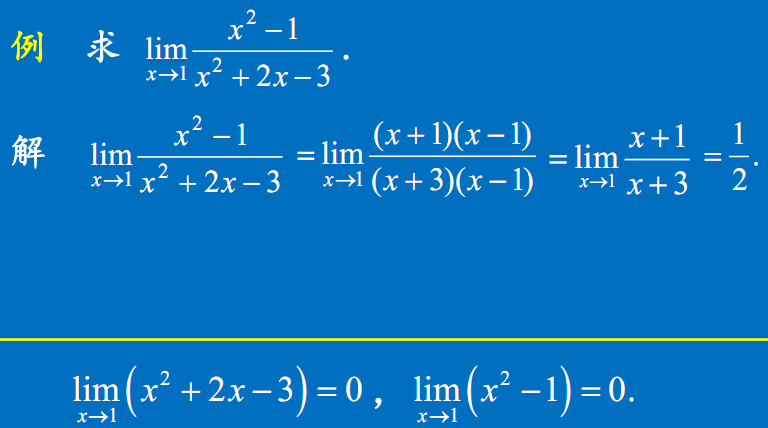
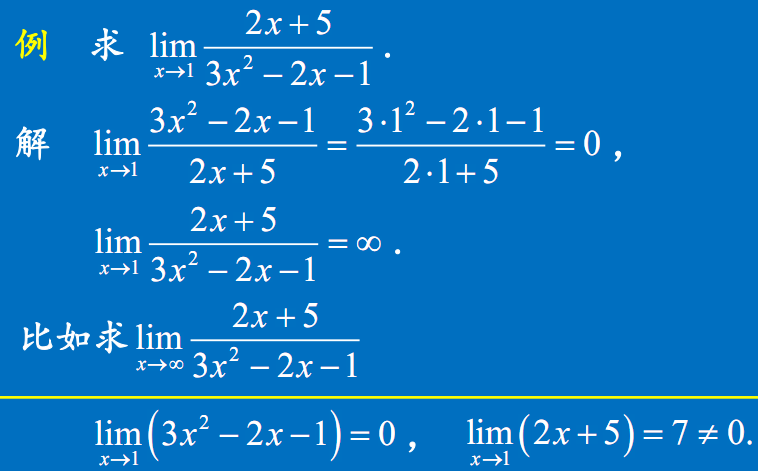
复合函数的极限运算法则
定理


实例
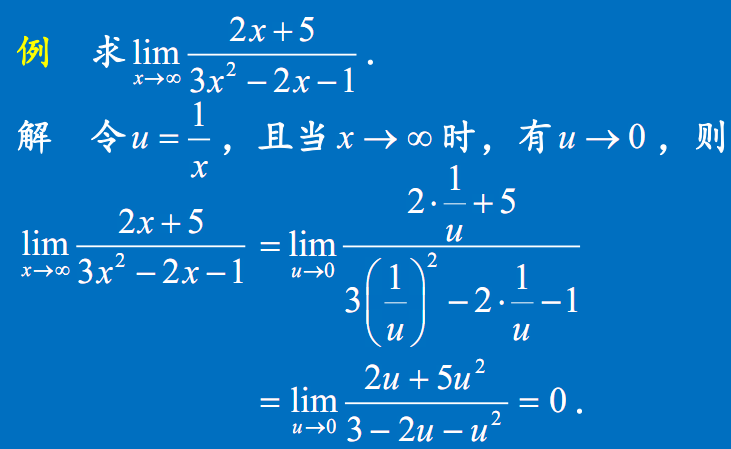
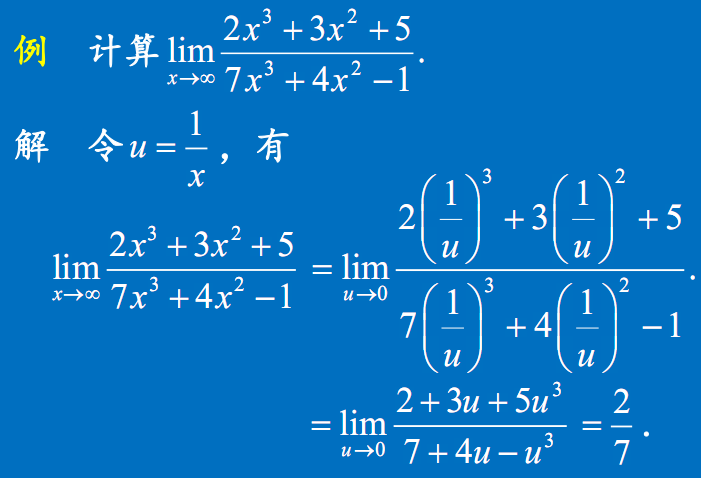
无穷比无穷型极限

本文链接: 1-5极限运算法则

