1-10区间上连续数的性质

在闭区间上连续

如果函数f(x)在开区间(a,b)内连续,且在左端点a右连续,在右端点b左连续,则称函数f(x)在闭区间[a,b]上连续

最大值最小值定理与有界性定理

最大值最小值

最大值最小值定理

闭区间上连续的函数在该区间上一定存在它的最大值和最小值

有界性定理

闭区间上连续的函数在该区间上必有界

例1

例2

零点定理与介值定理

零点

方程$f(x)=0$的根称作函数$f(x)$的零点

零点定理

设函数f(x)在闭区间[a,b]上连续,且$f(a)\cdot f(b)<0$,则至少存在一点$\xi \in(a,b)$,使 $f(\xi)=0$

零点定理的几何意义

条“有头有尾”连续不断的曲线弧,其一头位于x轴的下方,而另一头位于x轴的上方,那么它一定会与x轴相交.当然,可能交点还不止一个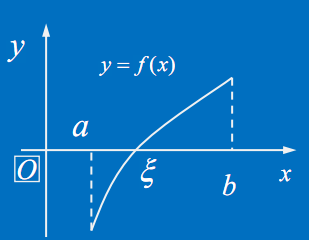

例题

介值定理

介值定理的几何意义

习题

习题1

解:

连续函数有界性定理:闭区间上连续的函数在该区间上必有界

习题2

最大最小值定理:闭区间上连续的函数在该区间上一定存在它的最大值和最小值

习题3

因为a和b是两个相邻的实根，首先是实根，其次是相邻，这说明a和b之间的函数图像要么在x轴上方，要么在x轴下方。
又之间有一点c是的$f(x)>0$,这说明函数图像在x轴上方，则(a,b)内f(x)恒大于0，如果有d,使得f(d)小于0的情况的话，则(a,b)之间，函数图像势必要穿过一次x轴，这样a,b就是不是相邻的根了。而是a,d是相邻的根。

总结: 连续函数,相邻的根之间的函数值符号相等，要么同时大于0，要么同时小于0

习题4

由零点定理:设函数f(x)在闭区间[a,b]上连续,且$f(a)\cdot f(b)<0$,则至少存在一点$\xi \in(a,b)$,使 $f(\xi)=0$

可以看到零点定理有两个条件，一个条件是闭区间上连续，一个是两个端点异号，所以选C

习题5

解:函数是初等函数，定义域$D=( -\infty,+\infty)$,$f(0)=0-asin0-b=-b$,(0,a+b]是定义区间
因为b>0，所以，$f(0)=-b<0$
$f(a+b)=a+b-asin(a+b)-b=a-asin(a+b)=a(1-sin(a+b))$,
由$-1\le sinx \le 1$得，$-1+1 \le -sin(x)+1 \le 1+1$,
即 $0 \le -sin(x)+1 \le 2$，所以$0 \le 1-sin(a+b) \le 2$,
所以$0 \le a(1-sin(a+b)) \le 2a$
即 $0 \le f(a+b) \le 2a$
所以$f(0)\cdot f(a+b) \le 0$
满足两个条件，满足零点定理，至少有一个实根

本文链接: 1-10区间上连续数的性质