微分的定义
微分的几何意义
基本初等函数的微分公式与微分运算法则

微分的定义

引例

定义

可导等价于可微分

$dy=f’(x_0)\Delta x$,$dx=\Delta x$

例题求增量对应的微分

微分的几何意义

在点M1的附近,我们可以用切线段来近似代替曲线段。

基本初等函数的微分公式与微分运算法则

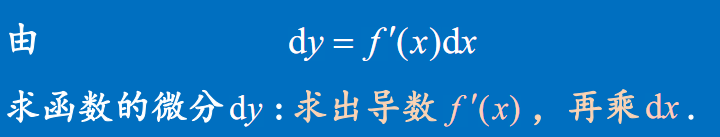
由$dy=f’(x)dx$求函数的微分dy:求出导数$f’(x)$,再乘$dx$

基本初等函数的微分公式

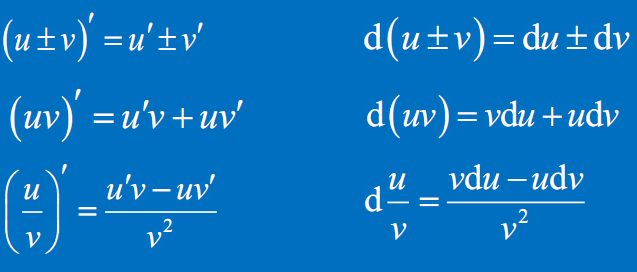
函数和差积商的微分运算法

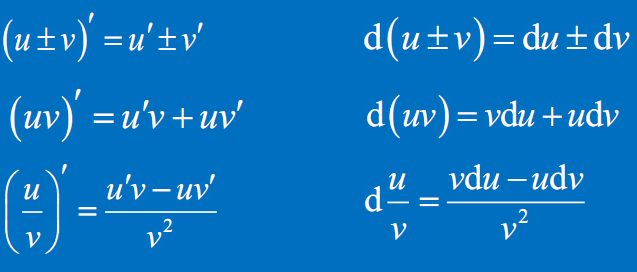
复合函数的微分法则

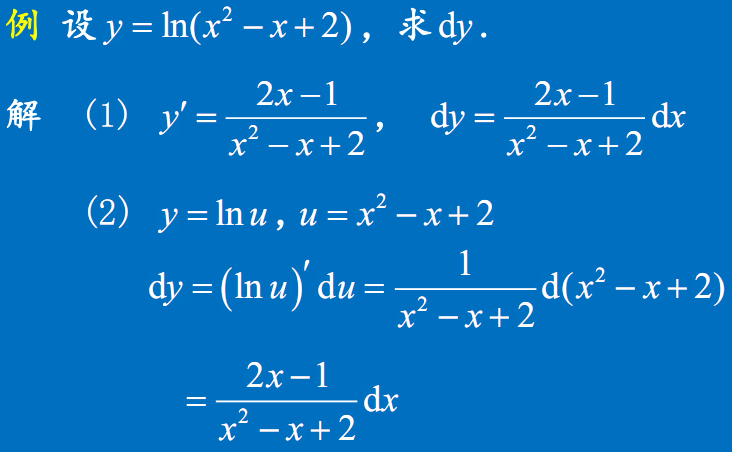
习题

题1-1

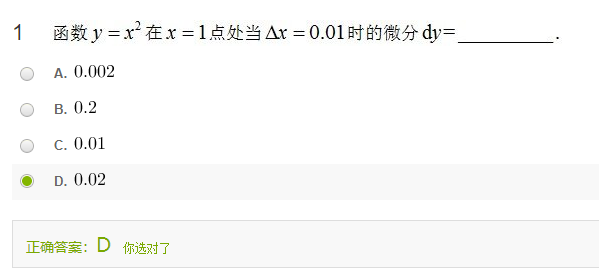
解:这题考微分的定义式:
$dy=f’(x_0)\Delta x$,$dx=\Delta x$
所以:
$y’=2x$
$dy=\left. y’\right|_{x=1 }\Delta x=2\times 1\times 0.01=0.02$

题1-2

$dy=y’dx=\dfrac{y\cos x +\sin (x-y)}{\sin (x-y)-\sin x }dx$
解:
方程两本同时对$x$求导得:
$$
\begin{aligned}
y’\sin x +y\cos x -(-\sin (x-y)\times (1-y’))=&0 \nonumber \\
y’\sin x +y\cos x +(\sin (x-y)\times (1-y’))=&0 \nonumber \\
y’\sin x +y\cos x +\sin (x-y)-y’\sin (x-y)=&0 \nonumber \\
y’(\sin x -\sin (x-y)) +y\cos x +\sin (x-y)=&0 \nonumber \\
\end{aligned}
$$
得到:
$$
\begin{aligned}
y’=&\dfrac{-(y\cos x +\sin (x-y))}{(\sin x -\sin (x-y))} \nonumber \\
y’=&\dfrac{y\cos x +\sin (x-y)}{\sin (x-y)-\sin x } \nonumber \\
\end{aligned}
$$
所以$dy=y’dx=\dfrac{y\cos x +\sin (x-y)}{\sin (x-y)-\sin x }dx$

题1-3

$\left.dy\right\vert_{x=1}=\left.y’\right\vert_{x=1}dx=(1-e)dx$
导数公式:$(\sqrt{x})’=\dfrac{1}{2\sqrt{x}}$
$$
\begin{aligned}
\left. y’\right\vert_{x=1}=&\left. (2\dfrac{1}{2\sqrt{x}}-e^x)\right\vert_{x=1} \nonumber \\
=&\dfrac{1}{\sqrt{1}}-e^1 \nonumber \\
=&1-e \nonumber \\
\end{aligned}
$$
所以:
$\left.dy\right\vert_{x=1}=\left.y’\right\vert_{x=1}dx=(1-e)dx$

题1-4

$$
\begin{aligned}
dy=&y’dx \nonumber \\
=&(-\dfrac{1}{x^2}+\dfrac{1}{\sqrt{x}})dx \nonumber \\
\end{aligned}
$$
导数公式:
$(\sqrt{x})’=\dfrac{1}{2\sqrt{x}}$
$(\dfrac{1}{x})’=-\dfrac{1}{x^2}$
所以:
$$
\begin{aligned}
y’=&\dfrac{1}{x}+2\sqrt{x} \nonumber \\
=&-\dfrac{1}{x^2}+\dfrac{1}{\sqrt{x}} \nonumber \\
\end{aligned}
$$
所以
$$
\begin{aligned}
dy=&y’dx \nonumber \\
=&(-\dfrac{1}{x^2}+\dfrac{1}{\sqrt{x}})dx \nonumber \\
\end{aligned}
$$

题1-5

选C
$(\dfrac{3}{2} x^2)’=\dfrac{3}{2} 2x=3x$

本文链接: 2-5函数的微分