测验1
题1
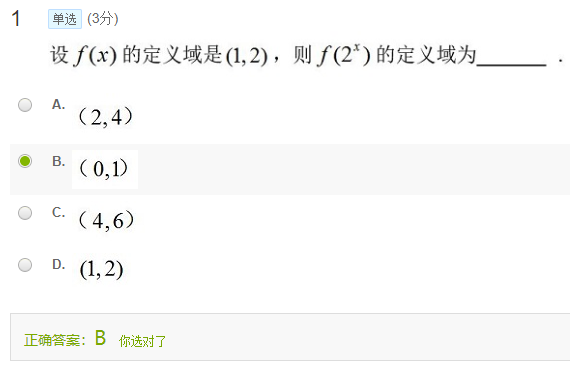
$y=2^x$是增函数,$2^0=1< 2^x <2=2^1$,
所以 $0<x<1$.
题2
$$
\begin{align}
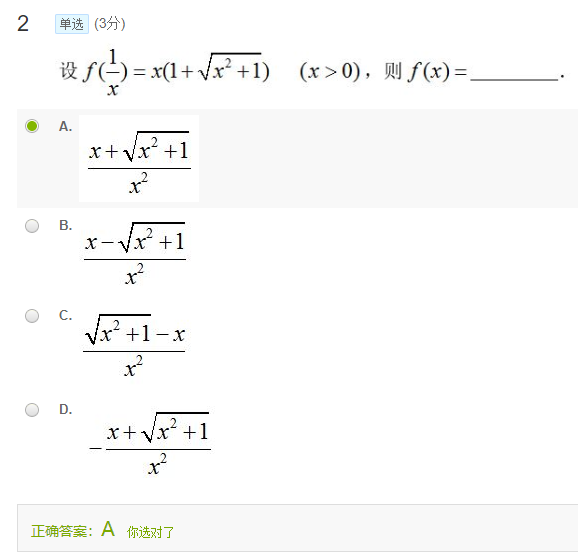
&f(\dfrac{1}{x}) \nonumber \\
=&f(x^{-1}) \nonumber \\
=&x(1+\sqrt{x^2+1}) \nonumber \\
\end{align}
$$
所以
$$
\begin{align}
f(x)=&f((x^{-1})^{-1}) \nonumber \\
=&x^{-1}(1+\sqrt{(x^{-1})^2+1}) \nonumber \\
=&x^{-1}(1+\sqrt{x^{-2}+1}) \nonumber \\
=&x^{-1}(1+\sqrt{\dfrac{1}{x^2}+\dfrac{x^2}{x^2}}) \nonumber \\
=&x^{-1}(1+\sqrt{\dfrac{1+x^2}{x^2}}) \nonumber \\
=&x^{-1}(1+\dfrac{\sqrt{1+x^2}}{x}) \nonumber \\
=&\dfrac{1}{x}(\dfrac{x+\sqrt{1+x^2}}{x}) \nonumber \\
=&(\dfrac{x+\sqrt{x^2+1}}{x^2}) \nonumber \\
\end{align}
$$
题3

$cos(x)$是周期函数,周期为$2\pi$,所以$cos2n\pi=cos2\pi=1$
$cos(2n\pi)$是初等函数,所以,极限值就等于函数值等于1
题4

当n为奇数时,$[(-1)^n+1]=2$,所以$\lim \limits_{n \to \infty}2\dfrac{n-1}{n}=2$
当n为偶数时,$[(-1)^n+1]=0$,所以$\lim \limits_{n \to \infty}2\dfrac{n-1}{n}=0$
所以极限不存在
题5

数列数列收敛则其子数列收敛,但是子数列收敛不能退出数列是否收敛。
题6

解: 先来看反比例函数的图像
$\lim \limits_{x \to 0 }2^{\dfrac{-1}{x}}$
这题求左右极限,
先求右极限:$\lim \limits_{x \to 0^+ }2^{\dfrac{-1}{x}}$,
令$u(x)=\dfrac{-1}{x}$,则$\lim \limits_{x \to 0^+ }u(x)=\dfrac{-1}{x}=- \infty $
,所以$\lim \limits_{x \to 0^+ }2^{\dfrac{-1}{x}}
=\lim \limits_{u(x) \to -\infty }2^{u(x)}=0$
再来求左极限:$\lim \limits_{x \to 0^- }2^{\dfrac{-1}{x}}$
令$u(x)=\dfrac{-1}{x}$,则$\lim \limits_{x \to 0^- }u(x)=\dfrac{-1}{x}=+ \infty $
左极限不等于右极限,所以极限不存在
题7

解:y=x^2函数图像,
$\lim \limits_{x \to 0 }f(x)=\lim \limits_{x \to 0 }x^2=0$,排除A
$\lim \limits_{x \to -1^- }f(x)=\lim \limits_{x \to -1^- }x^2=1$,正确
$\lim \limits_{x \to 1^- }f(x)=\lim \limits_{x \to 1^- }x^2=1$
$\lim \limits_{x \to 1^+ }f(x)=\lim \limits_{x \to 1^+ }0=0$ 排除D
所以$\lim \limits_{x \to 1 }f(x)$不存在 排除C
题8

解:cosx是震荡函数,不存在极限,排除C
$x \to +\infty$时,$-x \to -\infty$ 所以,$\lim \limits_{x \to \infty^+ }2^{-x}=2^{-\infty}=0$
$x \to -\infty$时,$-x \to +\infty$,所以$\lim \limits_{x \to \infty^+ }2^{-x}=2^{+\infty}=+\infty$
左右极限不想的,所以不存在极限,所以排除D
符号函数图像
符号函数$|sgnx|\le 1$,$\lim \limits_{x \to \infty }\dfrac{1}{x}=0$,所以$\lim \limits_{x \to \infty }\dfrac{sgnx}{x}=0$,有界函数与无穷小的乘积是无穷小
题9

解:
$$
\begin{align}
&\lim \limits_{x \to \infty }(\dfrac{x^3}{x^2+1}-\dfrac{x^2}{x+1}) \nonumber \\
=&\lim \limits_{x \to \infty }\dfrac{(x^3)(x+1)-(x^2)(x^2+1)}{(x^2+1)(x+1)} \nonumber \\
=&\lim \limits_{x \to \infty }\dfrac{(x^4+x^3)-(x^4+x^2)}{x^3+x^2+x+1} \nonumber \\
=&\lim \limits_{x \to \infty }\dfrac{x^3-x^2}{x^3+x^2+x+1} \nonumber \\
=&1 \nonumber \\
\end{align}
$$
题10

水平渐近线定义
$f(x)$水平渐近线,就是$\lim \limits_{x \to \infty }f(x)$的值
因为 $\lim \limits_{x \to \infty }\dfrac{1}{x^3-3x^2-7}=0$,$|sinx|\le 1$,所以:
$\lim \limits_{x \to \infty }\dfrac{sinx}{x^3-3x^2-7}=0$
有界函数与无穷小的乘积依然是无穷小
测验2
题1
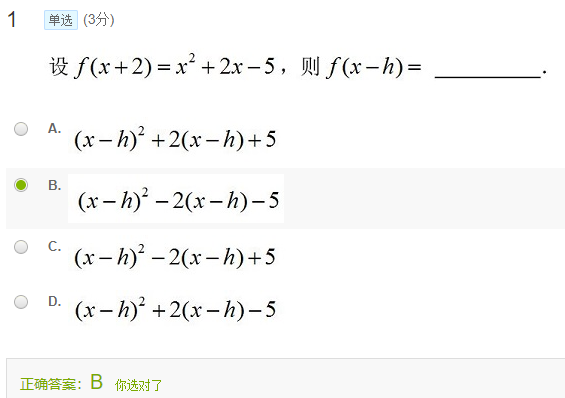
解:
由平方和公式:
$(x+2)^2=x^2+2\times2x+4$
令:
$f(x+2)=(x+2)^2+g(x)=x^2+2x-5$
得:
$$
\begin{align}
g(x)=&x^2+2x-5-(x^2+4x+4) \nonumber \\
=&-2x-9 \nonumber \\
=&-2x-2\times2+2\times2-9 \nonumber \\
=&-2(x+2)-5 \nonumber \\
\end{align}
$$
所以$f(x+2)=(x+2)^2+g(x)=(x+2)^2-2(x+2)-5$,
所以$f(x)=x^2-2x-5$
所以$f(x-h)=(x-h)^2-2(x-h)-5$
选B
题2

题3

这题考数列有界性定理
如果数列$x_n$收敛,则数列$x_n$一定有界,反之,如果数列有界,则其未必收敛;
推论:如果数列无界,则其一定发散;
无界一定发散,但是发散不一定无界,所以是充分非必要条件
题4
解:
$$
\begin{align}
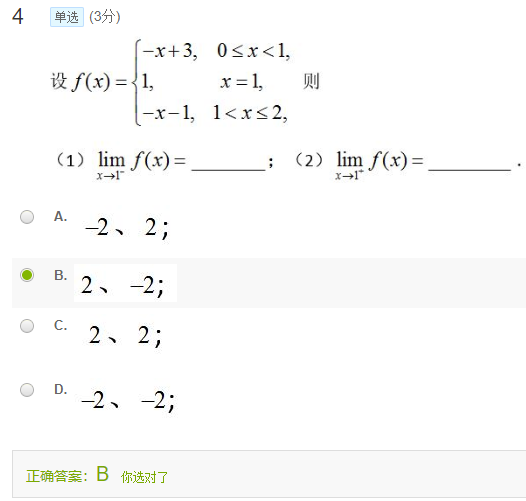
&\lim \limits_{x \to 1^- }f(x) \nonumber \\
=&\lim \limits_{x \to 1^- }(-x+3) \nonumber \\
=&-1+3 \nonumber \\
=&2 \nonumber \\
\end{align}
$$
$$
\begin{align}
&\lim \limits_{x \to 1^+ }f(x) \nonumber \\
=&\lim \limits_{x \to 1^+ }(-x-1) \nonumber \\
=&-1-1 \nonumber \\
=&-2 \nonumber \\
\end{align}
$$
题5

解:发比例函数$y=\dfrac{-1}{x}$图像在二四象限。
$\lim \limits_{x \to 0^- }\dfrac{-1}{x}=+\infty$
所以$\lim \limits_{x \to 0^- }2^{\dfrac{-1}{x}}=+\infty$
$\lim \limits_{x \to 0^+ }\dfrac{-1}{x}=-\infty$
所以$\lim \limits_{x \to 0^- }2^{\dfrac{-1}{x}}=0$
左右极限不存在,所以函数极限不存在
题6

解:由函数极限的局部有界性可知,极限存在可以退出局部有界。
但是局部有界不能退出极限存在,如$sinx$有界,但是$\lim \limits_{x \to -\infty }sinx$不存在
题7

解:
$$
\begin{align}
&\lim \limits_{x \to -2 }\dfrac{x^2-4}{x+2} \nonumber \\
=&\lim \limits_{x \to -2 }\dfrac{(x+2)(x-2)}{x+2} \nonumber \\
=&\lim \limits_{x \to -2 }(x-2) \nonumber \\
=&-4 \nonumber \\
\end{align}
$$
题8

解:因为$cosx$是震荡函数$\lim \limits_{x \to \infty }cosx$不存在,排除A
$|sgnx|\le 1$,是有界函数,$\lim \limits_{x \to \infty }\dfrac{1}{x}=0$,
所以当$x \to \infty $时,$\dfrac{1}{x}$为无穷小量,有界函数与无穷小量的乘积是无穷小量。所以极限存在且为0
$\lim \limits_{x \to +\infty }2^{-x}=2^{-\infty}=0$
$\lim \limits_{x \to -\infty }2^{-x}=2^{+\infty}=+\infty$
左右极限不相等,所以极限不存在
D极限为$ \infty $,本质上并不是极限。
题9

如果:$\lim \limits_{x \to \infty }f(x)=b$则y=b为曲线f(x)的水平渐近线,
如果:$\lim \limits_{x \to x_0 }f(x)= \infty $则$x=x_0$为曲线f(x)的垂(铅)直渐近线,
$\lim \limits_{x \to \infty }\dfrac{1}{x^3-3x^2-7}=0$,
$|sinx|\le 1$,所以$\lim \limits_{x \to \infty }\dfrac{sinx}{x^3-3x^2-7}=0$
有界函数与无穷小量的乘积是无穷小量
题10

解:$\lim \limits_{x \to \infty }\dfrac{2x^2+x+1}{x^2-1}=2$
所以水平渐近线为$y=2$
本文链接: 第一讲 测验

