网上习题

发表于 | 更新于 | 分类于 ， ，

函数定义域的求法

解题思路
(1)基本函数

  • 分式的分母≠0，
  • 对数的真数>0,
  • 偶次方根下的表达式≥0,
  • 反正弦、反余弦号内的表达式绝对值≤1
    (2)复合函数的定义域=简单函数的定义域所构成的不等式组的解集。

    习题

    求下列函数的定义域
    $y=arcsin\dfrac{1-x}{4}+\dfrac{\sqrt{1-lg(x-2)}}{x^2-3x-4}$
    解
    $$
    \begin{cases}
    \left| \dfrac{1-x}{4} \right| \le 1 \\
    1-lg(x-2) \ge 0 \\
    x-2 \gt 0 \\
    x^2-3x-4 \not =0
    \end{cases}
    $$
    (1) 先来解绝对值不等式：由$\left| \dfrac{1-x}{4} \right| \le 1$ 得：$-1\le \dfrac{1-x}{4}\le 1$ $\Rightarrow$ $-4 \le 1-x \le 4$ ,两边同时减1得到 $-5 \le -x \le 3$ 同时乘以$-1$ 得到: $5 \ge x \ge -3$,也就是 $-3 \le x \le 5$
    (2) 然后来解第二个等式:$1-lg(x-2) \ge 0$,得到$lg(x-2) \le 1$,也就是 $lg(x-2) \le lg(10)$,从而得到$x-2 \le 10$ ,所以$x \le 12$。
    (3) 然后是第三等式：得到$x \gt 2$
    (4) 第四个等式:$x^2-3x-4 \not =0$,令$x^2-3x-4 =0$，则
    $\Delta=\sqrt{b^2-4ac}=\sqrt{(-3)^2-4 \times 1 \times(-4)}=\sqrt{9+16}=\sqrt{25}=5$,
    所以，$x_1,x_2=\dfrac{-b \pm \Delta}{2a}=\dfrac{-(-3) \pm 5}{2\times 1}=\dfrac{3 \pm 5}{2}=4,-1$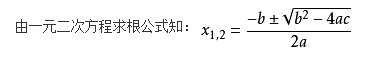

    当然解这等式也可以使用因式分解法，也就是十字相乘法。

    利用分解因式法解二元一次方程: 当二元一次方程的一边为0，而另一边分解成两个一次因式的乘积时，这种解二元一次方程的方法叫分解因式法。
    十字相乘法：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数。其实就是运用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。
    $$
    \begin{align}
    x^2-3x-4=0\\
    \end{align}
    $$

$$
\begin{matrix}
1_{a_1}\quad& & \quad -4_{c_1} \\
\quad& \times &\quad\\
1_{a_2}\quad& & \quad 1_{c_2} \\
\end{matrix}
$$
$a=1=a_1\times a_2=1\times1$,
$c=-4=c_1\times c_2=(-4)\times1$,
$b=-3=a_1\times c_2+a_2 \times c_2=1\times 1+1\times (-4)=-3$,所以满足十字相乘法，
分解因式为$(x-4)(x+1)=0$,解得$x_1=4,x_2=-1$,所以$x\not=4,x\not=-1$

综上:
$$
\begin{cases}
-3 \le x \le 5 \\
x \le 12 \\
x \gt 2 \\
x\not=4,x\not=-1
\end{cases}
$$
画出数轴，求出三个交集为$(2,4) \cup (4,5)$

函数解析式的求法

Latex语法

1
\Delta

显示效果:$\Delta$

二元运算

乘法

1
\times

$\times$

正负号

1
\pm

$\pm$

矩阵

1
2
3
4
5
6
7
$$
  \begin{matrix}
   1 & 2 & 3 \\
   4 & 5 & 6 \\
   7 & 8 & 9
  \end{matrix} \tag{1}
$$

$$
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix} \tag{1}
$$

交集

1
A交B：$A\cap B$，A并B：$A\cup B$

A交B：$A\cap B$，A并B：$A\cup B$

参考文献

大学高等数学第一章函数(习题精讲)
高中函数解析式的求法
CSDN_Markdown 使用LaTeX写矩阵

本文链接: 网上习题

0%