自动控制原理拉式变换

拉氏变换复习

拉普拉斯变换

$L[\dfrac{d}{dt}f(t)]=sF(s)-f(0)$
$L[\dfrac{d^2}{dt^2}f(t)]=s^2F(s)-sf(0)-f’(0)$

1 2	$L[\dfrac{d}{dt}f(t)]=sF(s)-f(0)$ $L[\dfrac{d^2}{dt^2}f(t)]=s^2F(s)-sf(0)-f'(0)$

拉普拉斯反变换

通常首先进行部分分式展开,然后查表求拉氏反变换。

序号	拉式变换
1	$L[1(t)]= \dfrac{1}{s}$
2	$L[t]= \dfrac{1}{s^2}$
3	$L[\dfrac{1}{2} t^2]=\dfrac{1}{s^3}$
4	$L[e^{-at}]=\dfrac{1}{s+a}$
5	$\sin bt\to \dfrac{b}{s^2+b^2}$
6	$\cos bt \to \dfrac{s}{s^2+b^2}$
7	$e^{-at}\sin bt\to \dfrac{b}{(s+a)^2+b^2}$
8	$e^{-at}\cos bt \to \dfrac{s+a}{(s+a)^2+b^2}$

幂函数的拉氏变换

公式:
$L[t^n]=\dfrac{n}{s}[t^{n-1}]$
$L[t^n]=\dfrac{n}{s}\cdot\dfrac{n-1}{s}\cdots\dfrac{2}{s}\cdot\dfrac{1}{s}\cdot L[t^0]=\dfrac{n!}{s^{n+1}}$
利用公式可得:

单位速度函数斜坡函数

斜坡函数,或者说单位速度函数:$
f(t)=\begin{cases}
0\quad &t\lt 0 \\
t\quad &t\ge0
\end{cases}
$,图像如下: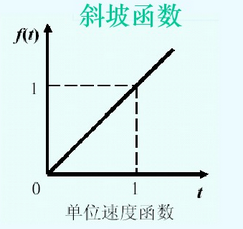

$L[t]=\dfrac{1}{s^2}$

单位加速度函数

单位加速度函数:$
f(t)=\begin{cases}
0\quad &t \le 0 \\
\dfrac{1}{2}t^2\quad &t \ge 0
\end{cases}
$,图像如下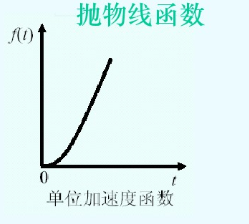

由$L[t^2]=\dfrac{2\times1}{s^{2+1}}=\dfrac{2}{s^3}$可得:
$L[f(t)]=L[\dfrac{1}{2}t^2]=\dfrac{1}{s^3}$

单位脉冲函数的拉氏变换

单位脉冲函数:$\delta(t)=\begin{cases}
0\quad &(t<0且t>\varepsilon) \\
\lim \limits_{\varepsilon \to 0 }\dfrac{1}{\varepsilon}\quad &(0<t<\varepsilon)
\end{cases}
$
图像如下: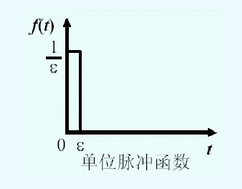

$L[\delta(t)]=1$