第一类换元公式
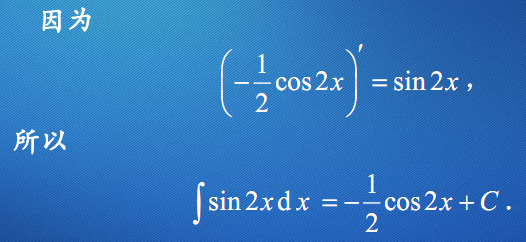
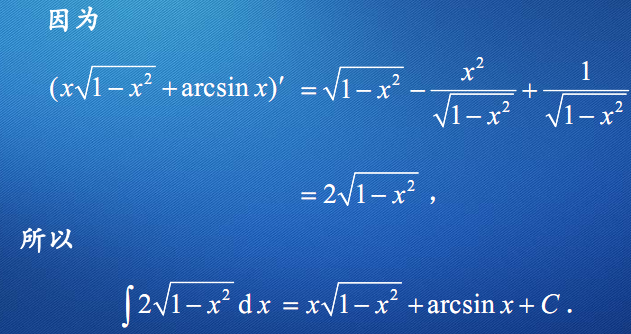
定理
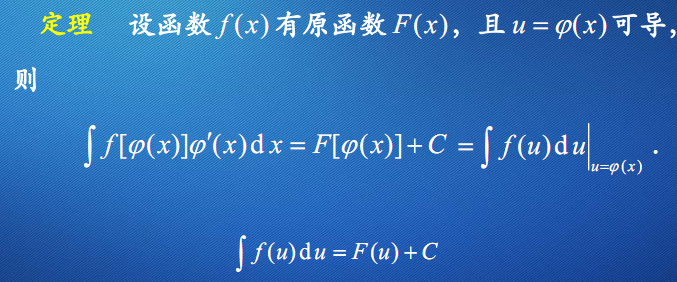

第一类换元法举例

例1
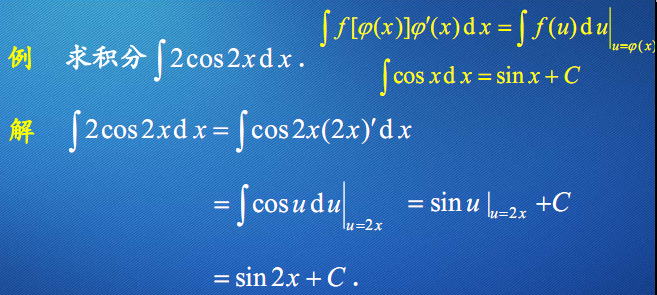
例2
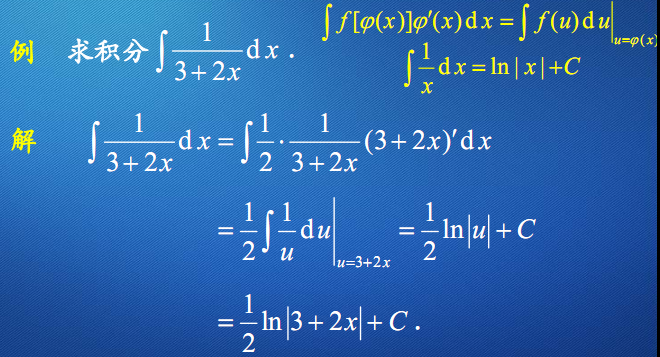
一次函数f(ax+b)的积分定理

$\int f(ax+b)dx=\dfrac{1}{a}F(ax+b)+C$
例3
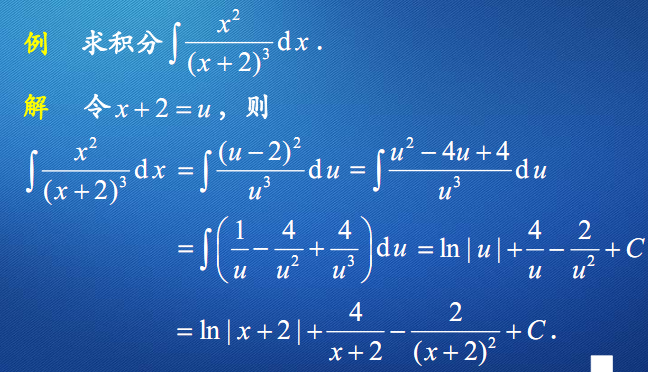
凑微分法

$\int f[\varphi(x)]d[\varphi(x)]=F[\varphi(x)]+C$
例4

例5

$\int x f(x^2)dx=\dfrac{1}{2}\int f(x^2)d(x^2)$
例6

$\int \dfrac{1}{a^2+x^2}=\dfrac{1}{a}\arctan \dfrac{x}{a}+C$
例7
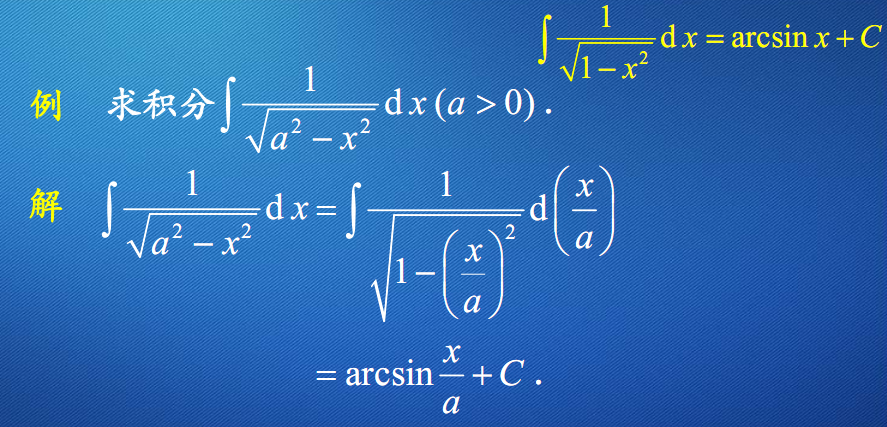
$\int \dfrac{1}{\sqrt{a^2-x^2}} dx=arcsin\dfrac{x}{a}+C$
例8

对数的运算性质:$\log_a\dfrac{M}{N}=\log_aM-\log_aN$
$\int \dfrac{1}{x^2-a^2}dx=\dfrac{1}{2a} \ln \left\vert \dfrac{x-a}{x+a} \right\vert+C$
例9
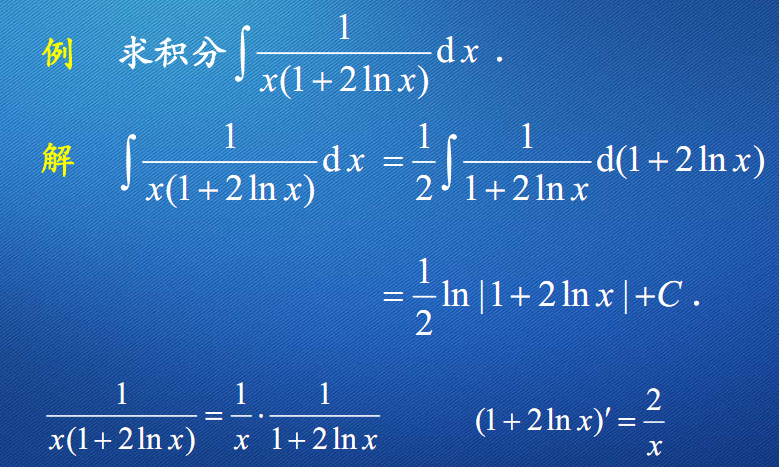
例10
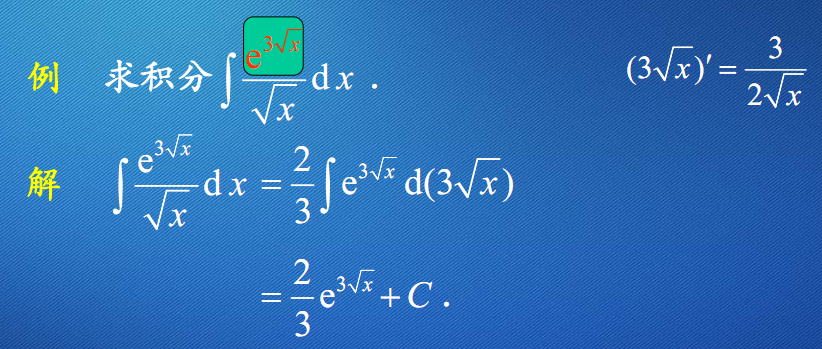
例11
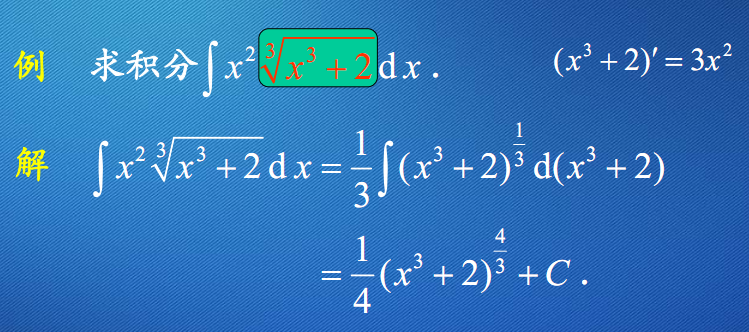
凑微分公式汇总
$\int f(ax+b)dx=\dfrac{1}{a}F(ax+b)+C$
$\int x f(x^2)dx=\dfrac{1}{2}\int f(x^2)d(x^2)$
不定积分公式
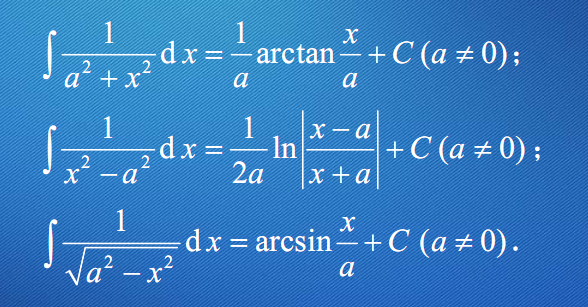
$\int \dfrac{1}{a^2+x^2}=\dfrac{1}{a}\arctan \dfrac{x}{a}+C$
$\int \dfrac{1}{\sqrt{a^2-x^2}} dx=arcsin\dfrac{x}{a}+C$
$\int \dfrac{1}{x^2-a^2}dx=\dfrac{1}{2a} \ln \left\vert \dfrac{x-a}{x+a} \right\vert+C$
本文链接: 4-3不定积分的第一类换元法

