第1题
已知单位反馈控制系统的前向通道传递函数为:$G(s)=\dfrac{K}{s^2(s+2)(s+4)}\quad K\ge 0$,画出系统的根轨迹图。
解
按下列步骤绘制根轨迹:
(1)系统开环有限零点为$z_1=-1$;开环有限极点为$p_1,_2=0,p_3=-2,p_4=-4$
(2)实轴上的根轨迹区间为$[-\infty,-4]$,$[-2,-1]$
(3)根轨迹的渐近线条数为$n-m=3$,渐近线的倾角为
$\phi_1=60°,\phi_2=180°,\phi_3=-60°$
渐近线与实轴的交点为:
$\zeta_a=\dfrac{\sum\limits_{i=1}^{n}p_i-\sum\limits_{i=1}^{m}z_i}{n-m}=-\dfrac{5}{3}$
所以得到闭环系统跟轨迹如下图所示: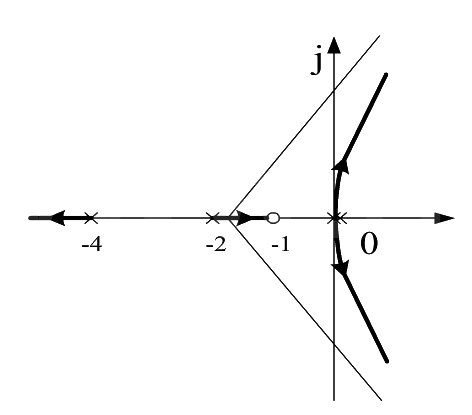
第2题
另一份答案4-14题
答案位置:https://www.docin.com/p-279144209.html第52页
题目
设单位负反馈系统的开环传递函数为$G(s)=\dfrac{K(s+4)}{s(s+2)}$试画出系统根轨迹图,并求出系统具有最小阻尼比时的闭环极点和对应的增益K
解
系统在实轴上的根轨迹区域为$[0,-2]$和$[4,-\infty)$
在这两段区域内,均存在分离点。为了求出分离点,令
$$
\dfrac{1}{d}+\dfrac{1}{d+2}=\dfrac{1}{d+4}
$$
解得:
$$
\begin{cases}
d_1=-4+2\sqrt{2}=-1.1172 \\
d_2=-4-2\sqrt{2}=-6.828
\end{cases}
$$
因而复数根轨迹是以$(-4,j0)$为圆心,$2\sqrt{2}$为半径的一个圆,如下图所示: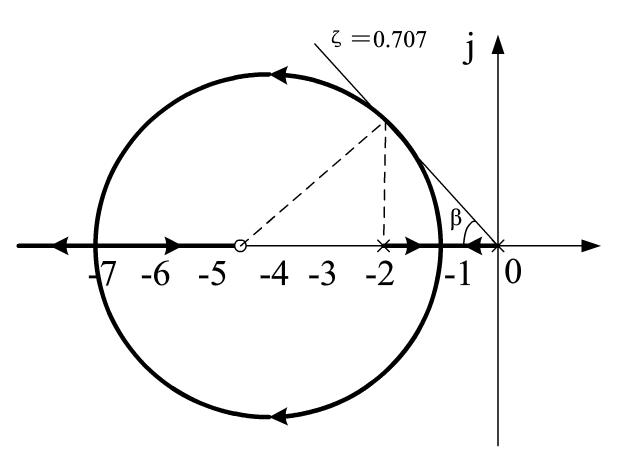
在图上,过原点作圆得切线,得最小阻尼比线。由根轨迹图知,对于等腰直角三角形,必有:
$\beta=45°$,故最小阻尼比:$\zeta=cos\beta=0.707$
响应的闭环极值点:$$s_1,_2=-2\pm j2$$
由根轨迹模值条件,可求出相应的增益为:
$$ K= \dfrac{\left\vert -2+j2 \right\vert \left\vert -2+j2+2 \right\vert}{\left\vert -2+j2+4 \right\vert}=2$$
原文链接: null

