概率
概率—表示事件A发生可能性大小的数值,称为事件A的概率,记为$P(A)$
注意:概率是随机事件的函数
古典概率的定义
若试验的样本空间S满足:
- 只有有限个样本点一有限性,
- 每个样本点发生的可能性相等一等可能性
称此试验为古典概型试验
古典概率的计算公式
在古典概型下,事件A的概率定义为:
$P(A)=\dfrac{A所含样本点数}{S含样本点总数}$
这里计算样本点数的主要工具是排列、组合
排列与组合
加法原理
设完成一件事有m种方式,第一种方式有$n_1$种方法,第二种方式有$n_2$种方法,……第m种方式有$n_m$种方法.则完成这件事总共有$n_1+n_2+\cdots+n_m$种方法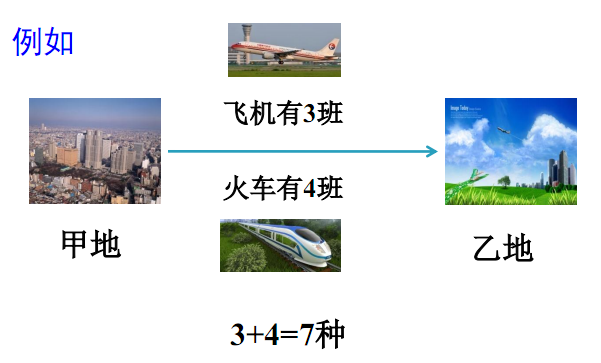
乘法原理
设完成一件事必须经过$r$个步骤:
第一个步骤有$n_1$种方法,第二个步骤有$n_2$种方法,第三个步骤有$n_3$种方法,……第r个步骤有$n_r$种方法。
则完成这件事总共有$n_1\times n_2 \times \cdots \times n_r$种方法
例题
例如,小王要从三种不同水果和两种不同饮料中各选一个,他有多少种不同选法?
排列和组合的区别
- 组合不管顺序
- 顺序不同则是不同的是排列
元素无重复(不放回)排列
全排列
(1)将n个不同元素按照一定次序排成一列,称为全排列,全排列的个数为:
$n!=n(n-1)(n-2)\cdots 2\times1$
例1
3个不同字母a,b,c的全排列个数为$3!=3×2×1=6$.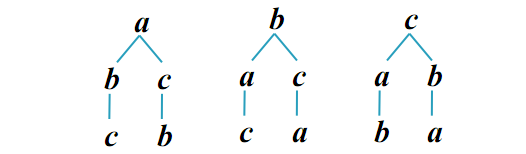
例2
从3个不同的球中取出2个的排列有?种
部分排列
(2)从n个不同元素中任取k个(1≤k≤n)元素排成一列,不同的排列总数为
例1
5个小孩排成一排的方式有多少种?
解: $5!=5×4×3×2×1=120$种
例2
将10本书任意放在书架上,求其指定的3本书靠在一起的排法有多少种?
解:$8!\times 3!=241920$种,这题需要两个步骤,排列这三本书,有$3!$种,然后把这三本书作为一个整体和剩下的7本书,进行排列,有$(1+7)!=8!$种
元素允许重复(有放回)的排列
(3)从n个不同元素中取k个($1≤k≤n$)排成一列(元素允许重复)不同排列的总数为:
$n\cdot n\cdots n=n^k$
例题
从盒中有放回地取3个球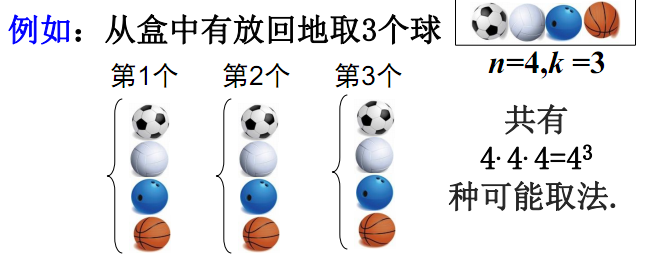
组合
单个组合
(1)组合:从n个不同元素中取$k(1≤k≤n)$个元素组成一组,(无次序)称为一个组合,所有组合的个数为:
例子
从3个不同的球中取出2个的组合有?种,(无次序)
多个分组
(2)n个不同元素分为k个$(1≤k≤m)$不同组,每组元素个数分别为$r_1$,$r_2$,$\cdots$,$r_k$个的分法总数为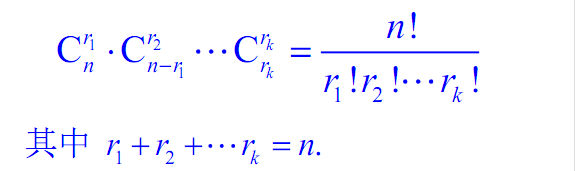
例子
例4将7个学生安排到一个三人间和两个双人间中住宿,问有多少种不同的住法?
解 问题转化为将7人分为3组,第1组有3人,第2组有2人,第3组有2人,不同住法总数为:
$C_7^3C_{7-4}^2C_2^2=\dfrac{7\times 6\times 5}{3\times2\times1}\dfrac{4\times 3}{2\times1}\dfrac{2\times1}{2\times1}=210$
古典概率的计算公式
在古典概型下,事件A的概率定义为:
$P(A)=\dfrac{\text{A所包含的样本点总数}}{\text{S所包含的样本点总数}}$
古典概率例题
例1
一批产品中有10个正品和2个次品,任意抽取两次,每次抽出一个,抽出后不放回,求第二次抽到次品的概率?
首先这里有第一次,第二次的区分,也就是跟顺序有关,所以用排列公式。
第二次抽到次品,抽取两次,有以下两种可能的情况(加法):
- 有第一次抽到次品,第二次抽到次品,分为两个
步骤(用乘法而不是加法):先从10个正品中取出一个,再从2个次品中取出一个,所以可能的结果为:$A_{10}^1A_2^1$。 - 第一次没有抽到次品,第二次抽到次品这两种可能,可能的结果为$A_2^2$。
所以事件包含的样本为$A_{10}^1A_2^1 + A_2^2$
样本空间S所包含的样本数为:$A_{12}^2$
例2

这里把人放到房间,把球放到格子之类的问题是排列问题。将$r$个人随机地分配到$n$个房间里,$r≤n$,所以样本空间为:$n^r$
例3
袋中有a个黑球,b个白球,若随机地(不放回)把球一个接一个地摸出来,求A“第k次摸出的球是黑球”的概率$(k≤a+b)$

这题我看不是很懂,第k次摸出来的是黑球,就用黑球数目除以总球数。
古典概率的性质

(1) 一个事件的概率大于等于0小于等于1
(2) 必然事件的概率为1
(3) 互斥事件(AB=$\emptyset$),如果两个事件互斥,则这两个事件的和事件的概率等于两个事件的概率之和,互斥事件的和事件的概率等于这些事件的概率之和。

(4)事件的概率和它的逆事件的概率的和为1,逆事件的概率等于1减去该事件的概率
(5)不可能事件的概率为0
(6)如果B事件包含事件A,则B事件的概率大于等于事件A的概率,B事件与A事件的差事件的概率等于B事件的概率减去A事件的概率
(7)事件A-B的概率等于A的概率减去A和B的交集的概率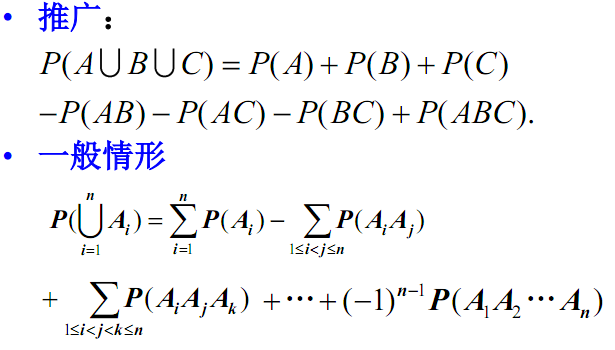
习题
习题1
随机地掷一骰子两次,两次出现的点数之和等于随 8的概率为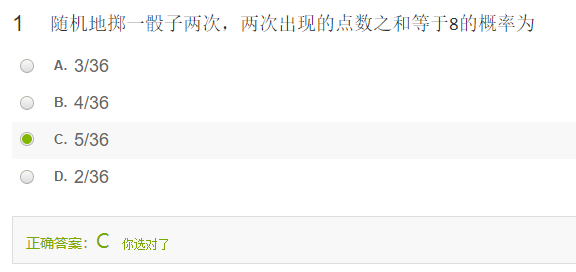
解:这是排列问题,是允许重复的排列.一个骰子有1,2,3,4,5,6这六种点数,两个点数的和的样本为:(2,6),(3,5),(4,4),(5,3),(6,2)这5中可能的结果,而两次有$6^2=36$种可能的结果.所以$P(A)=\dfrac{5}{36}$
习题2
n张奖券中含有m张有奖的,k个人购买,每人一张,其中至少有一人中奖的概率为
至少有一个人中奖的逆事件为没有人中奖,没有人中奖,则从n-m中没有奖的彩票中取出给这k个人。C_{n-m}^k
所以没有人中奖的概率为$P_1=\dfrac{C_{n-m}^k}{C_n^k}$
所以至少有一个人中奖的概率为$1-P_1=1-\dfrac{C_{n-m}^k}{C_n^k}$
习题3
某乒乓球队有9名队员,其中两名种子选手。现在要选5名队员参赛,则两名种子选手必须在内的概率为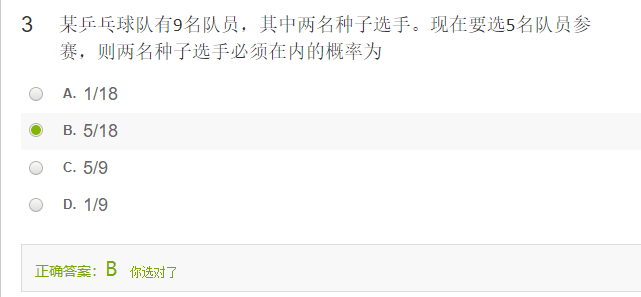
$P(A)=\dfrac{C_2^2C_7^3}{C_9^5}=\dfrac{1\times \dfrac{7\times 6\times 5}{3\times 2\times 1}}{\dfrac{9\times 8\times 7\times 6\times 5}{5\times 4\times 3\times 2\times 1}}$
分子分母同时乘以$5 \times \times 4\times 3\times 2 \times 1$消去各自的分母得到:
$P(A)=\dfrac{7\times 6\times 5 \times 5\times 4}{9\times 8\times 7\times 6\times 5}=\dfrac{5\times 4}{9\times 8}=\dfrac{5}{9\times 2}=\dfrac{5}{18}$
习题4
设有设 10个零件,其中2个次品,现随机抽取2个,恰有1个是正品的概率为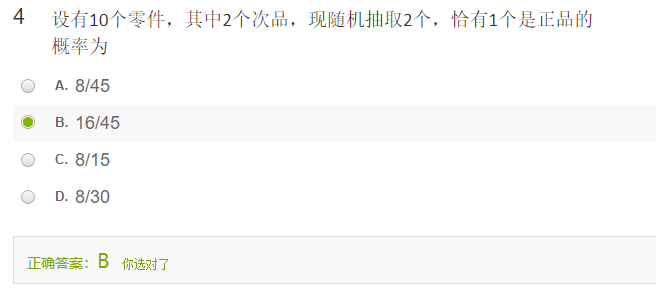
解:这是组合问题,恰有(只有)一个正品的意思是:从8个正品中先取出一个,然后再从2个次品中取一个。
$P(A)=\dfrac{C_8^1C_2^1}{C_{10}^2}=\dfrac{8 \times 2}{\dfrac{10\times 9}{2\times 1}}=\dfrac{8 \times 2}{5\times 9}\dfrac{16}{45}$
习题5
书架上按任意次序摆着15本教科书,其中有5本是数学书,从中随机地抽取3本,至少有一本是数学书的概率是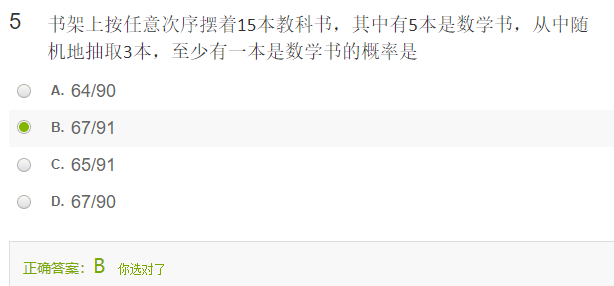
解:至少有一本,表示有1本,2本,或者3本。
$$
\begin{align}
P(A)&=\dfrac{C_5^1C_{10}^2+C_5^2C_{10}^1+C_5^3}{C_{15}^3} \nonumber \\
&=\dfrac{(5\times \dfrac{10\times9}{2\times 1}+\dfrac{5\times 4}{2 \times 1}\times 10+\dfrac{5\times 4\times 3}{3\times 2\times 1})(3\times 2 \nonumber \\
\times 1)}{15\times 14\times 13} \nonumber \\
&=\dfrac{(5\times 10\times 9+5\times 4\times 10 +5\times 4)(3)}{15\times14\times13} \nonumber \\
&=\dfrac{(10\times9+4\times10+4)(5\times 3)}{15\times 14\times13} \nonumber \\
&=\dfrac{(10\times9+4\times10+ 4)}{14\times13} \nonumber \\
&=\dfrac{(5\times 9+2\times10+2)(2)}{2\times7\times13} \nonumber \\
&=\dfrac{5\times 9+2\times10 +2}{7\times13} \nonumber \\
&=\dfrac{45+20+2}{70+21} \nonumber \\
&=\dfrac{67}{91} \nonumber \\
\end{align}
$$
习题6
抽签与次序有关,是否正确?
抽签与次序无关,看清题目
习题7
两封信随机地投向标号为1,2,3,4的四个邮筒,问第2个邮筒恰好投入一封信的概率3/8为, 是否正确?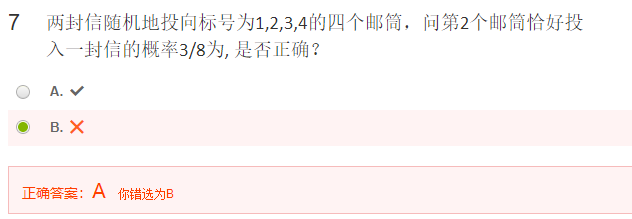
解这是有顺序的,是排列问题,
一封信放入一个邮筒的情况
首先先从两封信中取出一封放到2号油桶中,C_2^1,剩下的一封信,随意在剩下的三个邮筒中排列,A_3^1
$P(A)=\dfrac{C_2^1A_1^1+C_1^1A_3^1}{A_4^2}=\dfrac{2+3}{4\times3}=\dfrac{5}{12}$
邮筒中也有可能投入两封信
这题真操蛋,我还搞不懂先留着
本文链接: 第1周 第3讲 古典概率

