第1题
自动控制原理完整版课后习题答案pdf5-3,相似题目
设系统结构图如图所示,试确定输入信号$r(t)=sin(t+30°)$作用下,系统的稳态误差$e_ss(t)$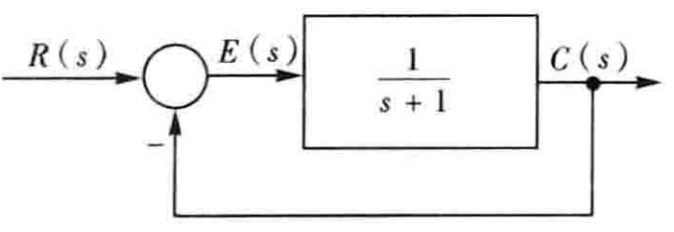
知识点
误差传递函数,频率特性的定义
先求出系统的误差传递函数,得到其幅频特性和相频特性,再根据频率特性的定义求出系统的稳态误差$e_{ss}(t)$。
解
系统的误差传递函数为:
$$
\Phi_e(s)=1-\Phi(s)=1-\dfrac{\dfrac{1}{s+1}}{1+ \dfrac{1}{s+1}}=\dfrac{s+1}{s+2}
$$
其幅频特性和相频特性分別为:
$\left\vert \Phi_e(j\omega) \right\vert= \sqrt{\dfrac{\omega^2+1}{\omega^2+4}}$,$\varphi_e(j\omega)=\arctan\omega-\arctan\dfrac{\omega}{2}$
当$r(t)=sin(t+30°)$时
$$
\begin{aligned}
e_{ss}(t)=&\sqrt{\dfrac{1+1}{1+4}}sin(t+30°+\arctan1-\arctan\dfrac{1}{2}) \\
=&\dfrac{\sqrt{10}}{5}sin(t+30°+45°-26.57°) \\
=&0.63sin(t+18.43°) \\
\end{aligned}
$$
第2题
自动控制原理完整版课后习题答案pdf5-8
已知系统开环传递函数$G(s)=\dfrac{10}{s(s/5+1)(s/200+1)}$,计算出截止频率
解
由题可得:
$G(j\omega)=\dfrac{10}{j\omega(\dfrac{j\omega}{5}+1)(\dfrac{j\omega}{200}+1)}$
则
$\left\vert G(j\omega) \right\vert=10\omega^{-1}(1+\dfrac{\omega^2}{25})^{-\frac{1}{2}}(1+\dfrac{\omega^2}{200^2})^{-\frac{1}{2}}$,
$\varphi(\omega)=-\dfrac{\pi}{2}-\arctan\dfrac{\omega}{5}-arctan\dfrac{\omega}{200}$
因此
$20\ln\left\vert G(j\omega) \right\vert=20-20\ln\omega-10\ln(1+\dfrac{\omega^2}{25})-10\ln(1+\dfrac{\omega^2}{200^2})$
对数频率特性曲线如下图所示: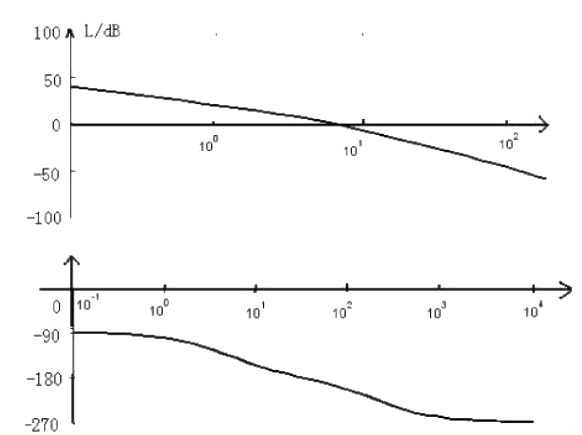
又$20ln\left\vert G(j\omega) \right\vert=0$,可得$\left\vert G(j\omega) \right\vert=2$,即$10\omega^{-1}(1+\dfrac{\omega^2}{25})^{-\frac{1}{2}}(1+\dfrac{\omega^2}{200^2})-\frac{1}{2}=1$
计算可得:$\omega_c=\sqrt{50}rad/s$
第3题
自动控制原理完整版课后习题答案pdf5-17
已知某最小相位系统的开环对数幅频特性如图所示,$L_1=8dB$,写出其开环传递函数。
解
(1)确定系统积分或微分环节的个数。
因对数幅频渐近特性曲线的低频渐近线的斜率为 $-20\gamma dB/dec$ ,
由图可知,低频渐近斜率为 $-40dB/dec$ ,故 $\gamma=2$ ,系统含有 $2$ 个积分环节。
(2)确定系统传递函数结构形式。由于对数幅频渐近特性曲线为分段折线,
其各转折点对应的频率为所含一阶或一阶环节的交接频率,
每个交接频率处斜率的变化取决于环节的种类。
- $\omega=\omega_1=0.5$ 处,斜率变化 $20dB/dec$ ,对应微分环节;
- $\omega=\omega_2=2$ 处,斜率变化 $-20dB/dec$ ,对应惯性环节;
- $\omega=\omega_2=5$ 处,斜率变化 $-20dB/dec$ ,对应惯性环节。
因此,所测系统具有下述传递函数:
$G(s)=\dfrac{K(1+T_1s)}{s^2(1+T_2s)(1+T_3s)}=\dfrac{K(1+\dfrac{1}{\omega_1}s)}{s^2(1+\dfrac{1}{\omega_2}s)(1+\dfrac{1}{\omega_3}s)}$
其中$K$待定。
(3)低频渐近线方程为
$L_a(\omega)=20\ln \dfrac{K}{\omega^{\gamma}}=20\ln K-20\gamma\ln\omega=20\ln K-40\ln\omega$
由$L_1(0.5)=8dB$,得到$K=10$
故所测系统传递函数为:
$G(s)=\dfrac{10(1+2s)}{s^2(1+0.5s)(1+0.2s)}$
第4题
自动控制原理完整版课后习题答案pdf5-13,第1小题()
已知系统开环传递函数G(s)(2s+1)(s+1),试根据奈氏判据,确定其闭环稳定时,K值的范围。
解
由系统的开环传递函数可知,系统的开环曲线图如下图所示: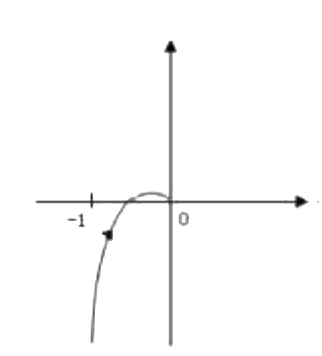
由于$P=0$,故想要闭环系统稳定,必有$N=0$,即幅相曲线不包围点$(-1,j0)$。
系统的频率特性表达式如下:
$G(j\omega)=\dfrac{K}{j\omega(2j\omega+1)(j\omega+1)}=\dfrac{-3K\omega^2+jK\omega(2\omega^2-1)}{(9\omega^4+\omega^2(2\omega^2-1)^2}$
对于开环幅相曲线与实轴的交点有:
$\dfrac{K\omega(2\omega^2-1)}{9\omega^4+\omega^2(2\omega^2-1)^2}=0$
由上式可得$\omega=\dfrac{\sqrt{2}}{2}$,则交点的实轴坐标为:
$\dfrac{-3K\omega^2}{(9\omega^4+\omega^2(2\omega^2-1)^2}>-1$
由上式可得$0<K<\dfrac{3}{2}$
第5题
自动控制原理完整版课后习题答案pdf5-14
某系统的开环传递函数为$Q(s)=\dfrac{K(T_2s+1)}{s^2(T_1s+1)}$,要求画出$0<2<T_1$下的奈奎斯特曲线,并判断闭环系统的稳定性。
解
当$0<T_2<T_1$时,
$Q(j\omega)=\dfrac{K(jT_2\omega+1)}{-\omega^2(1+jT_1\omega)}=\dfrac{K(1+T_1T_2\omega^2)+K\omega(T_2-T_1)}{-\omega^2(1+T_1^2\omega^2)}$
如果 $\omega=0_+$,则 $\left\vert Q(j0_+) \right\vert=\infty$,$\varphi(0_+)=-180°$
如果 $\omega=+\infty$,则 $\left\vert Q(j0_+) \right\vert=0$,$\varphi(0_+)=-180°$
其开环幅相曲线如下图所示: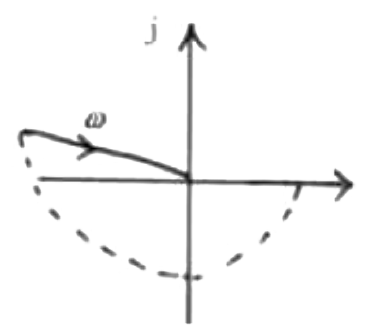
$P=0,N=-1$
则$Z=P-2N=2$,故系统不稳定
原文链接: null

