信号流图的基本性质
- 节点标志系统的变量,每个节点标志的变量是所有流向该节点的信号之代数和
- 支路相当于乘法器,信号流经支路时,被乘以支路增益而变换为另一信号
- 信号在支路上只能沿箭头单向传递,即只有前因后果的因果关系。
- 对于给定的系统,节点变量的设置是任意的,因此信号流图不是唯一的
信号流图常用名词术语
- 源节点(或输人节点):它一般代表系统的输入变量,故也称输入节点
- 阱节点(或输出节点) 它一般代表系统的输出,故也称输入节点
- 混合节点在混合节点上,既有输入支路又有输出支路。
- 前向通路:信号从输入节点到输出节点传递时,每个节点只通过一次的通路,叫前向通路
- 回路:起点和终点在同一节点
- 单独回路,简称回路,信号通过每一节点
不多于一次(0次或者1次)的闭合通路称为单独回路。 - 回路增益:回路中
所有支路增益之乘积叫回路增益,用$L_a$表示 - 不接触回路:回路之间没有公共节点时,这种回路叫不接触回路
信号流图的绘制
信号流图可以根据微分方程绘制,也可以从系统结构图按照对应关系得到
由系统微分方程绘制信号流图
任何线性方程都可以用信号流图表示
由系统结构图绘制信号流图
从系统结构图绘制信号流图时,
- 只需在结构图的信号线上用小圆圈标志出传递的信号,便得到节点;
- 用
标有传递函数的线段代替结构图中的方框,便得到支路,
于是,结构图也就变换为相应的信号流图了.
从系统结构图绘制信号流图时应尽量精简节点的数目。例如,支路增益为1的相邻两个节点,一般可以合并为一个节点,
在结构图比较点之前没有引出点(但在比较点之后可以有引出点)时,只需在比较点后设置一个节点便可
若在比较点之前有引出点时,就需在引出点和比较点各设置一个节点,分别标志两个变量,它们之间的支路增益是$1$
例2-13
例2-13试绘制图2-35所示系统结构图对应的信号流图:
解首先在结构图中标出节点,如下图紫色椭圆部分: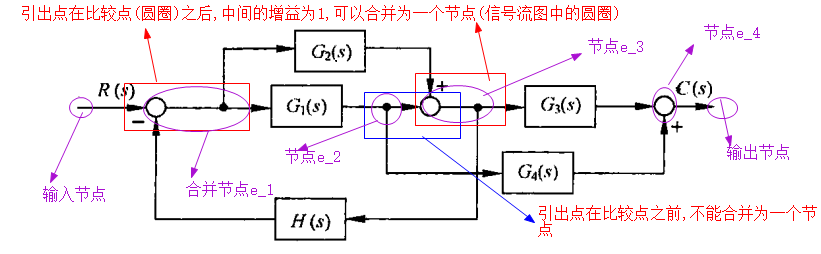
然后将各节点按原来顺序自左向右排列,将结构图中的方框用具有相应增益的支路代替,便得到系统的信号流图.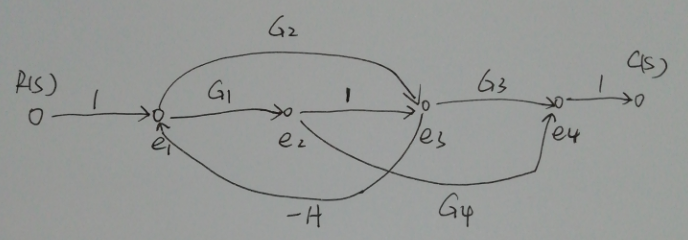
梅森增益公式
从一个复杂的系统信号流图上,经过简化可以求出系统的传递函数而且,结构图的等效变换
控制工程中常应用梅森( Mason)增益公式直接求取从源节点到阱节点的传递函数,而不需简化信号流图
具有任意条前向通路及任意个单独回路和不接触回路的复杂信号流图,求取从任意源节点到任意阱节点之间传递函数的梅森增益公式记为
$P=\dfrac{1}{\Delta}\sum\limits_{k=1}^{n}p_k\Delta_k$
式中,$P$为从源节点到阱节点的传递函数(或总增益);
$n$为从源节点到阱节点的前向通路总数;
$p_k$力为从源节点到阱节点的第$k$条前向通路总增益
$\Delta$为$1-\sum L_a+\sum L_aL_c-\sum L_dL_eL_f+\cdots$成为流图特征式
其中$\sum L_a$为所有单独回路增益之和
$\sum L_aL_c$为所有互不接触的单独回路中,每次取其中两个回路增益的乘积之和。
$\sum L_dL_eL_f$为所有互不接触的单独回路中,每次取其中三个的回路的增益的乘积之和
$\Delta_k$为流图余因子式,它等于流图特征式中除去与第$k$条前向通路相接触的回路的增益项(包括回路增益的乘积项)以后的余项式。
例2-14
例2-14试用梅森公式求例2-11系统的传递函数$C(s)/R(s)$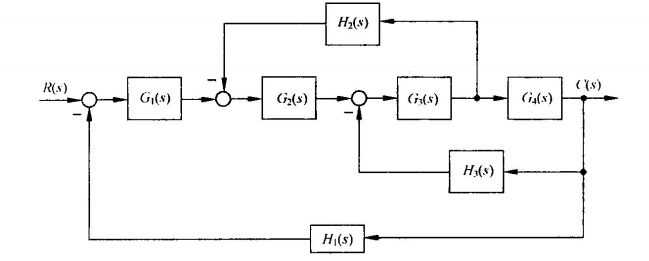
解:先标出节点(输入输出各自作为一个节点,比较点和引出点各自作为一个节点,这个图中没有需要合并的节点),如下图所示: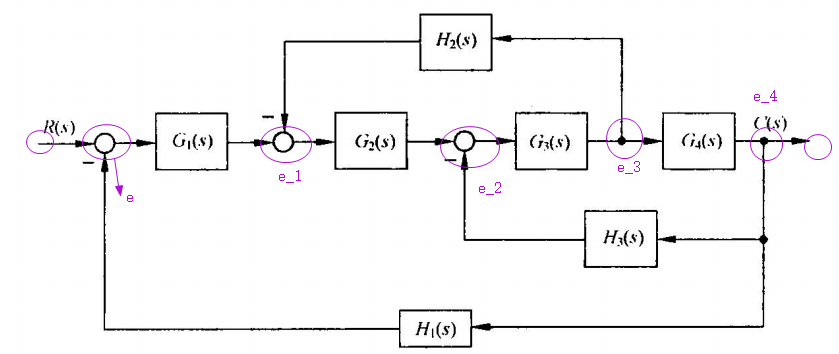
然后画出对应的信号流图如下图所示: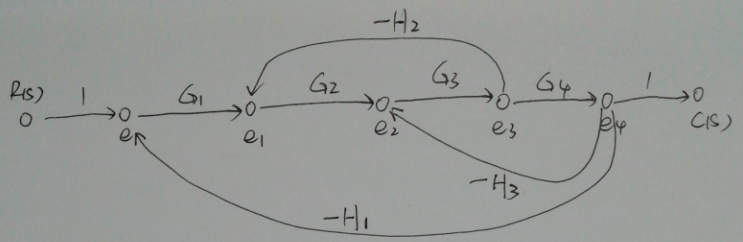
先来看前向通路:
前向通路只有$1$条:$R(s)\to e\to e_1\to e_2\to e_3\to e_4\to C(s)$,前向通路增益$p_1=G_1G_2G_3G_4$
再来看单独回路(每个节点走一次的回路):
单独回路1:$e\to e_1\to e_2\to e_3\to e_4\to e$,回路增益:$L_1=-G_1G_2G_3G_4H_1$
单独回路2:$e_1\to e_2\to e_3\to e_1$,回路增益:$L_2=-G_2G_3H_2$
单独回路3:$e_2\to e_3\to e_4$,回路增益:$L_3=-G_3G_4H_3$
三个回路都包含节点$e_2$,所以没有两两互不接触的回路,所以流图余子式:
$$
\begin{aligned}
\Delta=&1-\sum L_a+\sum L_bL_c-\sum L_dL_eL_f+\cdots \\
=&1-(L_1+L_2+L_3)+0-0\cdots \\
=&1+G_1G_2G_3G_4H_1+G_2G_3H_2+G_3G_4H_3 \\
\end{aligned}
$$
下面来求流图余子式$\Delta_1$,
因为前向通路:$R(s)\to e\to e_1\to e_2\to e_3\to e_4\to C(s)$
与回路1:$e\to e_1\to e_2\to e_3\to e_4\to e$有公共的节点:
$e,e_1,\cdots$,所以前向通路与该回路相接触
所以要在流图特征式$\Delta$中去除(减去)与该回路相关的增益项$L_1=-G_1G_2G_3G_4H_1$
同理前向通路与所有的单独回路都接触,所以也要减去相关的增益项$L_2,L_3$,
所以流图余子式$\Delta_1=\Delta-L_1-L_2-L_3=1$
答案
所以根据梅森增益公式,可以得到传递函数为:
$$
\begin{aligned}
\dfrac{C(s)}{R(s)}=&P \\
=&\dfrac{1}{\Delta}p_1\Delta_1 \\
=&\dfrac{G_1G_2G_3G_4\times 1}{1+G_1G_2G_3G_4H_1+G_2G_3H_2+G_3G_4H_3} \\
\end{aligned}
$$
例2-15
例2-15求图2-39所示系统的传递函数C(s)/R(s)。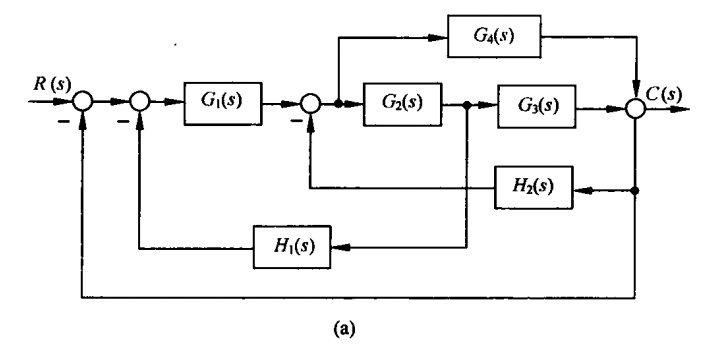
解,标出节点: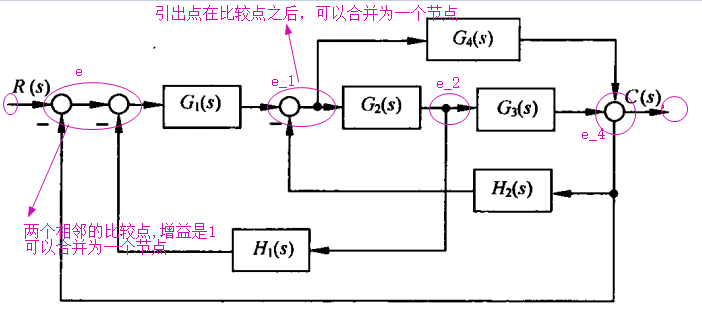
信号流图如下: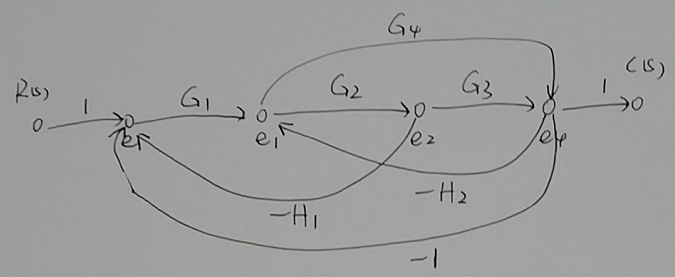
前向通路1:$R(s)\to e\to e_1\to e_2\to e_4\to C(s)$,前向通路增益$p_1=G_1G_2G_3$
前向通路2:$R(s)\to e\to e_1\to e_4\to C(s)$,前向通路增益$p_2=G_1G_4$
单独回路:
回路1:$e\to e_1\to e_2\to e$,增益$L_1=-G_1G_3H_1$
回路2:$e\to e_1\to e_4\to e$,增益$L_2=-G_1G_4$
回路3:$e\to e_1\to e_2\to e_4\to e$,增益$L_3=-G_1G_2G_3$
回路4:$e_1\to e_2\to e_4\to e_1$,增益$L_4=-G_2G_3H_2$
回路5:$e_1\to e_4\to e_1$,增益$L_5=-G_4H_2$
所有单独回路都包含节点$e_1$,所以流图特征式:
$$
\begin{aligned}
\Delta=&1-(L_1+L_2+L_3+L_4+L_5) \\
=&1+G_1G_3H_1+G_1G_4+G_1G_2G_3+G_2G_3H_2+G_4H_2 \\
\end{aligned}
$$
两条前向通路都包含节点$e_1$,所以前向通路与所有的单独回路都接触,所以流图余子式
$\Delta_1=1$,$\Delta_2=1$
答案
所以根据梅森增益公式,系统的传递函数为:
$$
\begin{aligned}
\dfrac{C(s)}{R(s)}=&\dfrac{1}{\Delta}(p_1\Delta_1+p_2\Delta_2) \\
=&\dfrac{G_1G_2G_3+G_1G_4}{1+G_1G_3H_1+G_1G_4+G_1G_2G_3+G_2G_3H_2+G_4H_2} \\
\end{aligned}
$$
例2-16
例2-16试求图2-40系统信号流图的传递函数$X_4/X_1$及$X_2/X_1$
对于给定的系统信号流图(或结构图),梅森增益公式中的特征式$\Delta$是确定不变的,只是对于不同的源节点和阱节点,其前向通路和余因子式是不同的。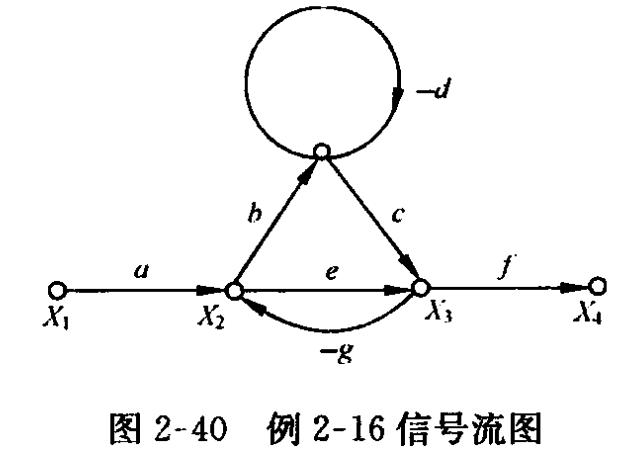
有三个单独回路:
$L_1=-d$
$L_2=-bcg$
$L_3=-eg$
则$\sum L_a=L_1+L_2+L_3=-d-bcg-eg$
$L_1$和$L_3$是互不接触的回路
则$\sum L_bL_c=L_1L_3=deg$
则流图特征式
$$
\begin{aligned}
\Delta=&1-\sum L_a+\sum L_bL_c \\
=&1+d+bcg+eg+deg \\
\end{aligned}
$$
从输入节点$X_1$到输出节点$X_4$有两条前向通路:
$p_1=aef$,该条前向通路与回路$L_2,L_3$接触,与回路$L_1$不接触,所以$\Delta_1=1+d$
和$p_2=abcf$,该条前向通路与所有的单独回路都接触,所以$\Delta_2=1$
答案1
所以输入节点$X_1$到输出节点$X_4$的传递函数为:
$$
\begin{aligned}
\dfrac{X_4}{X_1}=&\dfrac{1}{\Delta}(p_1\Delta_1+p_2\Delta_2) \\
=&\dfrac{aef(1+d)+abcf}{1+d+bcg+eg+deg} \\
\end{aligned}
$$
从输入节点$X_1$到输出节点$X_2$只有一个前向桶路,增益为$p_1=a$,相接触的回路有:回路2(-bcg),和回路3(-eg),所以
$\Delta_1=1+d$
答案2
所以从源节点$X_1$到输出节点$X_2$的传递函数为:
$\dfrac{X_2}{X_1}=\dfrac{p_1\Delta_1}{\Delta}=\dfrac{a(1+d)}{1+d+bcg+eg+deg}$
例2-17
例2-17试求图2-41信号流图中的传递函数$C(s)/R(s)$。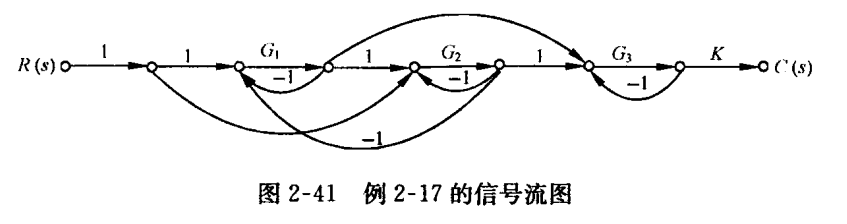
解题步骤
解这种题关键是要有耐心,把每个节点都标上记号: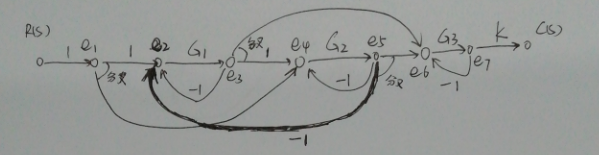
然后先来数单独回路: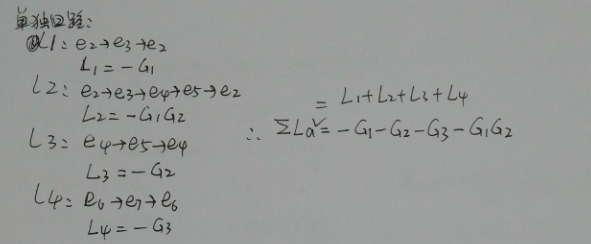
然后数两两互不接触回路(没有公共节点):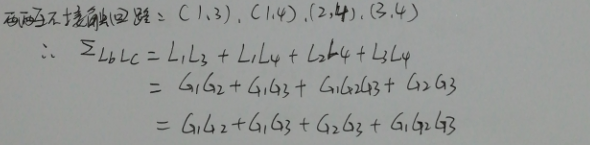
然后数三三互不接触回路: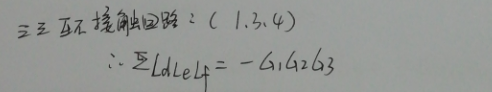
然后得到流图特征式: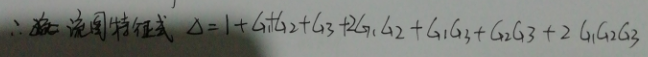
接下来找前向通路,一定要找全了:

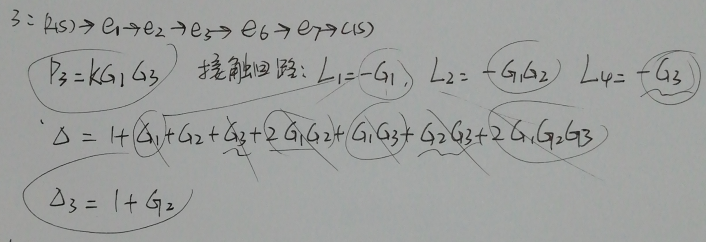

答案
最后代入梅森公式即可: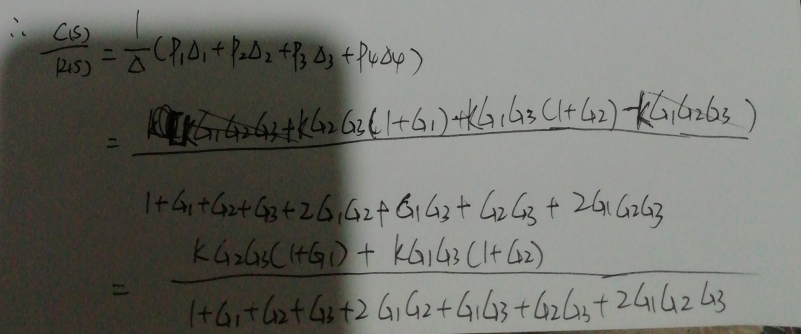
原文链接: 自动控制原理 信号流图的组成和性质

