导数公式汇总
常数和基本初等函数的导数公式

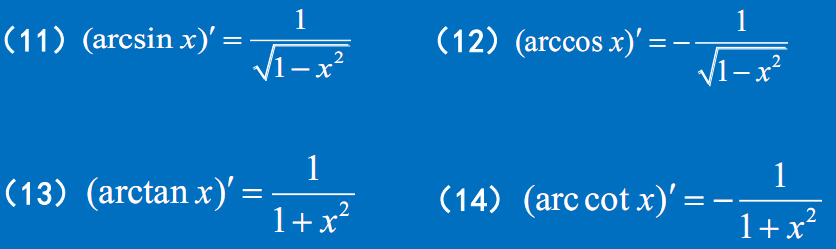
常数和基本初等函数的导数公式表
| 序号 | 导数公式 | 导数公式 |
|---|---|---|
| 1 | $(C)’=0$ | $(x^u)’=ux^{u-1}$ |
| 2 | $(a^x)’=a^x\ln a$ | $(e^x)’=e^x$ |
| 3 | $(log_ax)’=\dfrac{1}{x\ln a}$ | $(\ln x)’=\dfrac{1}{x}$ |
| 4 | $(\sin x)’=\cos x$ | $(\cos x)’=-\sin x$ |
| 5 | $(\tan x)’=\dfrac{1}{\cos^2x}=sec^2x$ | $(\cot x)’=-\dfrac{1}{\sin^2x}=-csc^2x$ |
| 7 | $\int \sec x\tan xdx=\sec x+C$ | $\int \csc x cot x dx=-cscx+C$ |
| 6 | $(\sec x)’=\sec x\tan x$ | $(\csc x)’=-\csc x\cot x$ |
| 7 | $(\arcsin x)’=\dfrac{1 }{\sqrt{1-x^2}}$ | $(\arccos x)’=-\dfrac{1 }{\sqrt{1-x^2}}$ |
| 8 | $(\arctan x)’=\dfrac{1}{1+x^2}$ | $(arccot x)’=-\dfrac{1}{1+x^2}$ |
- $x’=1$
- $(x^2)’=2x$
- $(\sqrt{x})’=\dfrac{1}{2\sqrt{x}}$
- $(\dfrac{1}{x})’=-\dfrac{1}{x^2}$
原文链接: 导数公式汇总

