等差数列
般地,如果一个数列从第2项起,每一项与它的前项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,通常用字母d表示,公差可以是正数,负数,也可以是0
通项公式
首项为$a_1$,公差为$d$的等差数列的通项公式是$a_n=a_1+(n-1)d$
通项公式变种:$a_n=a_m+(n-m)d$
$a_n=a+(n-1)d$,
$a_n-a_{n-1}=d$,$a_n=a_{n-1}+d$
等差中项
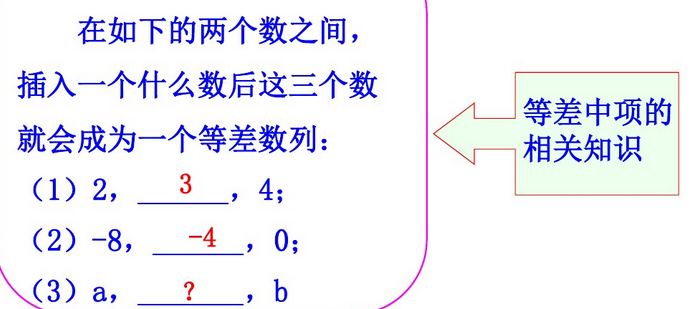
由三个数a,A,b组成的等差数列可以看成最简单的等差数列这时,A叫做a与b的等差中项.
$A= \dfrac{a+b}{2}$
等差数列前n项和公式
$S_n=\dfrac{n(a_1+a_n)}{2}=na_1+\dfrac{n(n-1)}{2}d$
等比数列
一般地,如果一个数列从第2项起,每项与它的前一项的比等于同一个常数,那么这个数列就叫做等比数列,这个常数叫做等比数列的公比(q)
通项公式:$a_{n+1}=a_nq$
$q=\dfrac{a_{n+1}}{a_n}$
等比数列前n项和公式
$S_n=\dfrac{a_1(1-q^n)}{1-q}=\dfrac{a_1-a_nq}{1-q}$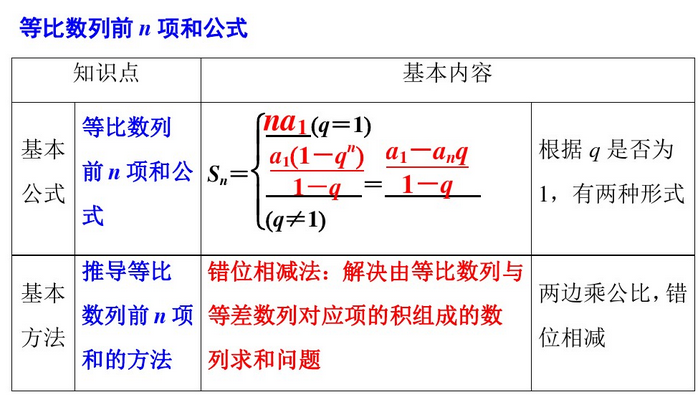
公式理解

参考资料
https://wenku.baidu.com/view/4f864251f12d2af90242e6dd.html?from=search
https://wenku.baidu.com/view/7016e507b207e87101f69e3143323968011cf428.html?from=search
https://wenku.baidu.com/view/194a9a6f960590c69fc3763c.html?from=search
本文链接: 数列前n项和公式

