引言
一、传递函数的定义和性质
二、传递函数的几种表达式
三、传递函数极点、零点对输出的影响
四、典型元部件的传递函数
传递函数的由来
- 对
初始条件为零的微分方程进行LapLace变换而来 - 利用元件部件的L表达式直接写出系统传递函数
使用传递函数的优点
- 使时域微分方程变成频域代数方程,减小问题的复杂度
- 了解系统参数或结构变化时系统动态过程的影响—分析
- 可以对系统性能的要求转化为对传递函数的要求—综合
- 整个经典控制理论建立在传递函数基础上。
传递函数的局限性
- 只适合
线性时不变系统,全零初始条件 - 只适用于解析计算,但不适用于数值计算
一、传递函数的定义和性质
传递函数的定义
1.定义:零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比
$G(s)=\dfrac{C(s)}{R(s)}$
其中$G(s)$成为传递函数
其中,$G(s)$称为传递函数,$C(S)=L\left( c(t) \right)$,$R(S)=L\left( r(t) \right)$零初始条件的两个含义
1) 指系统处于“稳态”,输出量及其各阶导数在T=0时为零
2) 指系统处于“静态”,输入量及其各阶导数在T<=0时为零
2. 传递函数与微分方程的关系
(1)传递函数由零初始条件微分方程经LapLace变换而得。
(2)如果将微分方程中的导数运算符用复变量s代换,可得
$\dfrac{d^k}{dt^k} \to s^k$
$r(t) \to R(s)$
$c(t) \to C(s)$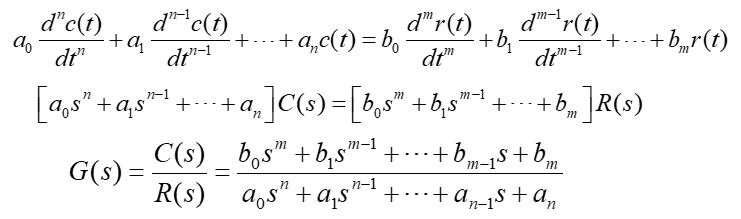
3.一般形式
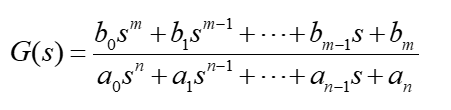
教材例2-8讲解
4.相应方块图
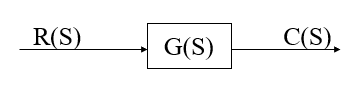
关于传递函数的几点说明
1) 传递函数概念适用于线性定常系统,它与线性常系数 微分方程一一对应,且与系统动态特性一一对应。
2) 传递函数不能反映系统或元件的学科属性和物理性质。物理性质和学科类别截然不同的系统可能具有完全相同的传递函数。研究某传递函数所得结论可适用于具有这种传递函数的各种系统。
3) 传递函数仅与系统结构和参数有关,与系统的输入无关。只反映了输入和输出之间的关系,不反映中间变量的关系。
4) 传递函数概念主要适用于单输入单输出系统。若系统有多个输入信号,在求传递函数时,除了一个有关的输入外,其它的输入量一概视为零。
5) 传递函数忽略了初始条件的影响。
6)传递函数传递函数是s的有理分式,对实际系统而言分母的阶次n大于分子的阶次m,此时称为n阶系统。
7) 传递函数$G(s)$的拉氏逆变换等于脉冲响应
8) 对输入信号导数的响应,等于系统对输入信号响应的导数,对输入信号积分的响应,等于系统对输入信号响应的积分
二、传递函数的几种表达式
1. 传递函数的“有理分式”型
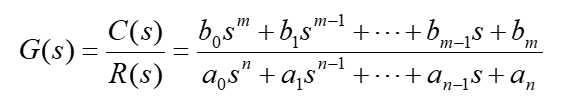
【说明】
- 由微分方程Laplace变换,结构图,信号流图综合及其他运算后的得到的
传递函数通常都写成有理式 - 分子分母多项式
以降幂的形式排列,各项系数多是实数 - 该形式在观察
初值、终值时特别直观 - 该形式在观察
稳态误差时也特别直观
2. 传递函数的零极点增益形式
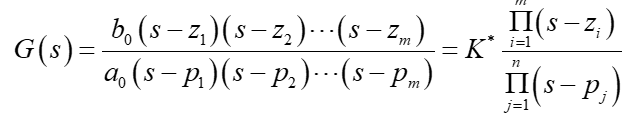
【说明】
- 分子分母写成“单阶因子”的形式
- $z_i$是传递函数的
零点,$p_j$ 是传递函数的极点,$ K*$为“零极 点型”增益或“根轨迹”增益 - 观察系统的
零极点分布最为方便
3. 传递函数的“标准因子”形式
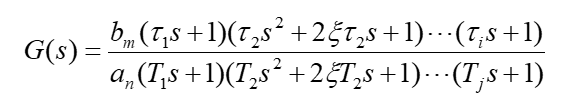
【说明】
- 分子分母均分解成“标准因子”乘积
- 各因子中,系数都是实数,且具有鲜明的物理概念
- 该形式适合绘制对
数幅频曲线(Bode) - 该形式适于观察
低频增益
4. 传递函数的“部分分式”形式
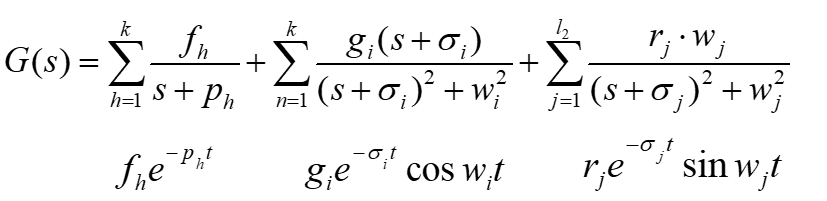
【说明】
- 传递函数被分解成“标准分式”的求和形式
- 分式中系数都是实数,且具有鲜明的物理概念
- 该形式适合通过Laplace反变换
求得时域响应
三、传递函数极点、零点对输出的影响
1.极点决定了固有响应的模态
说明:传递函数的极点就是特征方程的根, 决定了系统自由运动的模态, 在强迫运动(零初始条件响应)也包含这些模态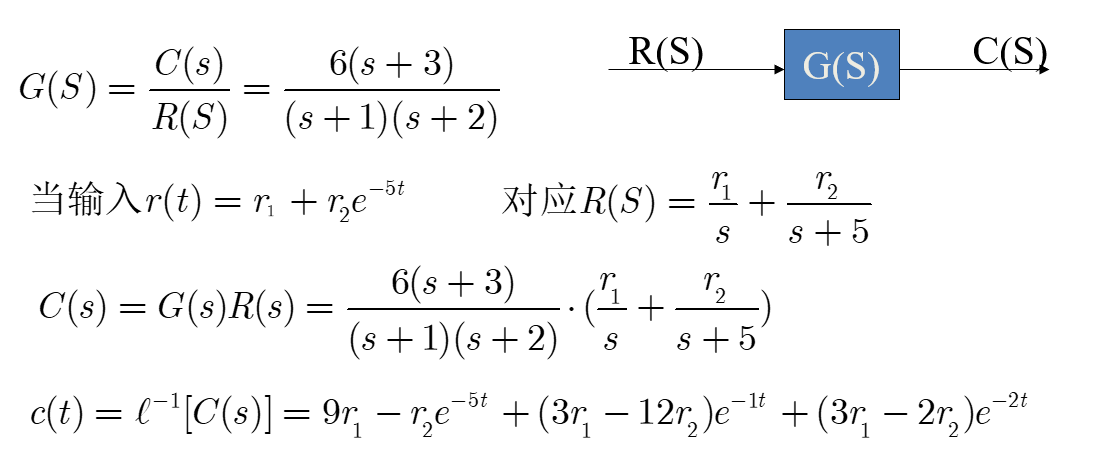
2.零点影响各模态在响应中所占的比重
举例,在单位阶跃输入下,观察极点相同而零点不同的两个系统响应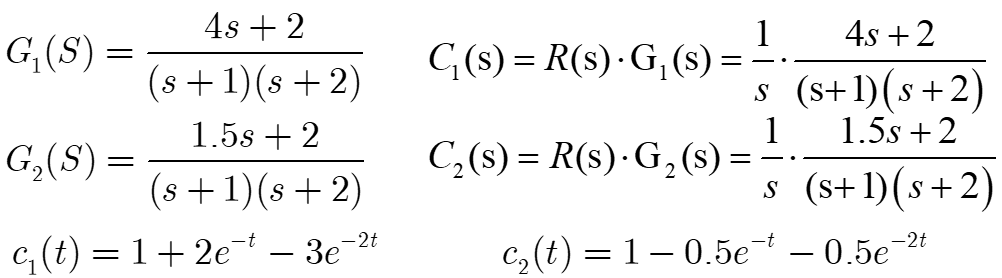
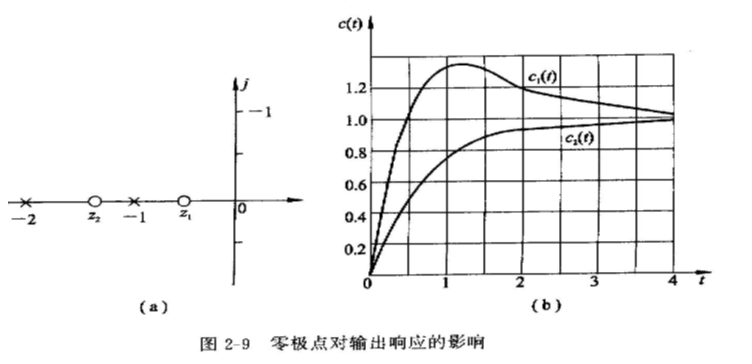
说明:传递函数的零点不影响系统自由运动的模态, 但影响各模态响应中占的比重, 因而影响曲线的形状.
本文链接: 2-2 复数域数学模型

