测验1
题1-1

$\lim \limits_{x \to \infty}\left(1+\dfrac{1}{x} \right)^x=e$,$\lim \limits_{x \to 0}\left(1+x\right)^\dfrac{1}{x}=e$
令$u=-2x$ 则 $x=\dfrac{-u}{2}$, 则
$x \to \infty$时,有$u \to \infty$
$\dfrac{x}{2}=\dfrac{-u}{2\times 2}=-\dfrac{1}{4}u$
所以:
$$
\begin{align}
&\lim \limits_{x \to \infty }(1+\dfrac{1}{-2x})^{\dfrac{x}{2}} \nonumber \\
=&\lim \limits_{u \to \infty }(1+u)^{-\dfrac{1}{4}u} \nonumber \\
=&\lim \limits_{u \to \infty }((1+u)^u)^{-\dfrac{1}{4}} \nonumber \\
=&(\lim \limits_{u \to \infty }(1+u)^u)^{-\dfrac{1}{4}} \nonumber \\
=&e^{-\dfrac{1}{4}} \nonumber \\
\end{align}
$$
知识点:常数C 乘方n 可以移到极限符号之外
题1-2
在同一过程中,有限个无穷小的代数和仍是无穷小
在同一过程中有极限的变量与无穷小的乘积是无穷小
常数与无穷小的乘积是无穷小
有限个无穷小的代数和仍是无穷小
有限个无穷小的乘积也是无穷小
因为$\alpha(x)$是无穷小,所以$\lim \limits_{x \to x_0 }sin[\alpha(x)]=sin0=0$,
所以$x \to x_0$时,$sin[\alpha(x)]$是无穷小量。排除答案A
$\alpha^2(x)-\beta ^2(x)$是无穷小(有限个无穷小的乘积也是无穷小,有限个无穷小的代数和仍是无穷小),排除答案C
$3\alpha(x)\beta ^2(x)$是无穷小(常数与无穷小的乘积是无穷小,有限个无穷小的乘积也是无穷小)排除答案D
$\beta ^2(x)$是无穷小,$\alpha(x)$是无穷小,而两个之比的极限有多种可能,所以选B
无穷小的比较 定义:
- 如果比的极限为:$1$,则两者是等价无穷小。
- 如果比的极限为:$0$,则$\beta ^2(x)$是比$\alpha(x)$高阶的无穷小。
- 如果比的极限为:$\infty $,则$\beta ^2(x)$是比$\alpha(x)$低阶的无穷小,
- 如果比的极限为:常数C,则是$\beta ^2(x)$与$\alpha(x)$是同阶无穷小。
题1-3

这题考无穷小的比较 定义:
$x \to 1$时 $(\sqrt{x}-1)$为无穷小,$1-x^3$为无穷小,求极限是要消去这些零因子
立方差公式:$a^3-b^3=(a-b)(a^2+ab+b^2)$
所以$1^3-x^3=(1-x)(1^2+x+x^2)=-(x-1)(1^2+x+x^2)$
$$
\begin{align}
&\lim \limits_{x \to 1 }\dfrac{\dfrac{1-x^3}{1+x} }{\sqrt{x}-1} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{1-x^3} {(1+x)(\sqrt{x}-1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(1-x^3)(\sqrt{x}+1)} {(1+x)(\sqrt{x}-1)(\sqrt{x}+1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{(1-x^3)(\sqrt{x}+1)} {(1+x)(x-1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{-(x-1)(1^2+x+x^2)(\sqrt{x}+1)} {(1+x)(x-1)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{-(1^2+x+x^2)(\sqrt{x}+1)} {(1+x)} \nonumber \\
=&\dfrac{-(1^2+1+1^2)(\sqrt{1}+1)} {(1+1)} \nonumber \\
=&-3 \nonumber \\
\end{align}
$$
所以是同阶无穷小
题1-4
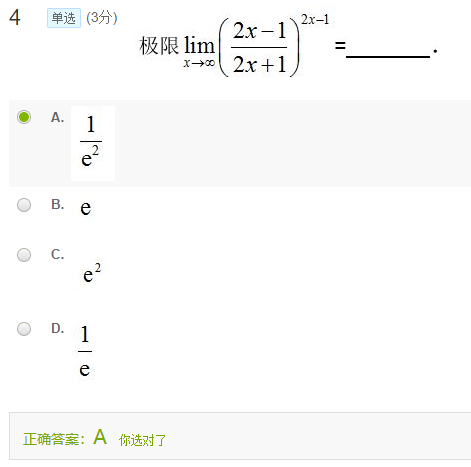
重要的极限:$\lim \limits_{x \to \infty}\left(1+\dfrac{1}{x} \right)^x=e$ , $\lim \limits_{x \to 0}\left(1+x\right)^\dfrac{1}{x}=e$
$2x-1=2x+1-1-1=2x+1-2$
$
\dfrac{2x-1}{2x+1}
=\dfrac{2x+1-2}{2x+1}
=1+\dfrac{-2}{2x+1}
$
令$\dfrac{1}{u}=\dfrac{-2}{2x+1}$
得$2x-1=-2u-2$,$x \to \infty $时,$u \to \infty $
所以
$$
\begin{align}
&\lim \limits_{x \to \infty }\dfrac{2x-1}{2x+1} \nonumber \\
=&\lim \limits_{u \to \infty }(1+\dfrac{1}{u})^{-2u-2} \nonumber \\
=&\lim \limits_{u \to \infty }(1+\dfrac{1}{u})^{-2(u-1)} \nonumber \\
=&(\lim \limits_{u \to \infty }(1+\dfrac{1}{u})^{(u-1)})^{-2} \nonumber \\
=&(\lim \limits_{u \to \infty }\dfrac{(1+\dfrac{1}{u})^u}{(1+\dfrac{1}{u})})^{-2} \nonumber \\
=&(\dfrac{\lim \limits_{u \to \infty }(1+\dfrac{1}{u})^u}{\lim \limits_{u \to \infty }(1+\dfrac{1}{u})})^{-2} \nonumber \\
=&\dfrac{e}{1}^{-2} \nonumber \\
=&e^{-2} \nonumber \\
=&\dfrac{1}{e^2} \nonumber \\
\end{align}
$$
整数指数幂的运算性质
题1-5

指数函数图像
反比例函数图像
$\lim \limits_{x \to 0^+ }\dfrac{1}{x}=+\infty$,所以$\lim \limits_{x \to 0^+ }(\dfrac{1}{5})^{\dfrac{1}{x}}=0$
$\lim \limits_{x \to 0^-}\dfrac{1}{x}=-\infty$,所以$\lim \limits_{x \to 0^- }(\dfrac{1}{5})^{\dfrac{1}{x}}=+\infty$
左右极限不相等,所以不正确,选A
题1-6

解:
$\lim \limits_{x \to 0^+ }f(x)=\lim \limits_{x \to 0^+ }x+1=1$,因为极限存在,所以左右极限相等。
$$
\begin{align}
&\lim \limits_{x \to 0^- }f(x) \nonumber \\
=&\lim \limits_{x \to 0^- }\dfrac{sinkx}{2x} \nonumber \\
=&\lim \limits_{x \to 0^- }\dfrac{kx}{2x} \nonumber \\
=&\dfrac{k}{2} \nonumber \\
=&\lim \limits_{x \to 0^+ }f(x) \nonumber \\
=&1 \nonumber \\
\end{align}
$$
所以$k=2$
题1-7

解:
$$
\begin{align}
&\lim \limits_{x \to 0^+ }x+3 \nonumber \\
=&3 \nonumber \\
=&\lim \limits_{x \to 0^- }\dfrac{arctan kx}{x} \nonumber \\
=&\lim \limits_{x \to 0^- }\dfrac{kx}{x} \nonumber \\
=&k \nonumber \\
\end{align}
$$
题1-8
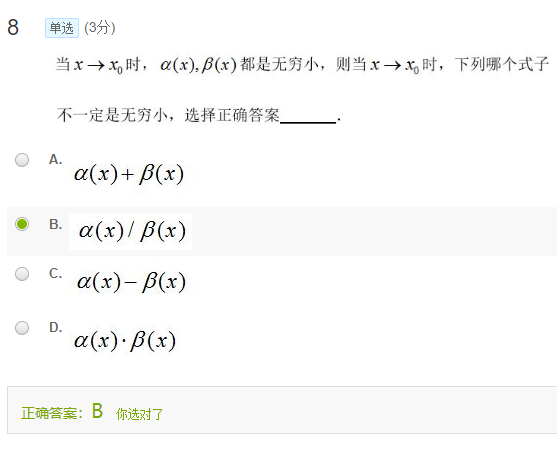
有限个无穷小的和是无穷小,所以排除A,C,
有限个无穷小的乘积是无穷小,所以排除D,
两个无穷小的商的极限有多种可能(1,0,无穷,常数),不不一定是无穷小(0)
题1-9

题1-10

等价无穷小公式:
- $1-cosx \sim \dfrac{1}{2}x^2$
- $tanx \sim x$
- $ tan\dfrac{x}{2} \sim \dfrac{x}{2}$
- $sinx \sim x$
$$
\begin{align}
&\lim \limits_{x \to 0^+ }f(x) \nonumber \\
=&\lim \limits_{x \to 0^+ }\dfrac{sinxtan\dfrac{x}{2}}{1-cos2x} \nonumber \\
=&\dfrac{x\dfrac{x}{2} }{\dfrac{1}{2}x^2} \nonumber \\
=&1 \nonumber \\
\end{align}
$$
$$
\begin{align}
&\lim \limits_{x \to 0^- }f(x) \nonumber \\
=&\lim \limits_{x \to 0^- }\dfrac{x+a}{2+e^{\dfrac{1}{x}}} \nonumber \\
=&\dfrac{0+a}{2+0} \nonumber \\
=&\dfrac{a}{2} \nonumber \\
=&1 \nonumber \\
\end{align}
$$
测验2
题2-1

重要的极限:
$\lim \limits_{x \to \infty}\left(1+\dfrac{1}{x} \right)^x=e$,$\lim \limits_{x \to 0}\left(1+x\right)^\dfrac{1}{x}=e$
本题中 $x \to 0$,所以这里要先构造出第个2公式的形式
首先构造括号中的内容:
令$u=-kx$,
$x \to 0$时,$u \to 0$,$x=\dfrac{u}{-k}$,
$\dfrac{1}{x}=\dfrac{1}{\dfrac{u}{-k}}=\dfrac{1}{u}\times -k$
得到指数:
$\sqrt[4]{e}=e\dfrac{1}{4}$
所以
$$
\begin{align}
&\lim \limits_{x \to 0 }(1-kx)^{\dfrac{1}{x}} \nonumber \\
=&\lim \limits_{u \to 0 }(1+u)^{\dfrac{1}{u}\times -k} \nonumber \\
=&(\lim \limits_{u \to 0 }(1+u)^{\dfrac{1}{u}})^{-k} \nonumber \\
=&e^{-k} \nonumber \\
=&e\dfrac{1}{4} \nonumber \\
\end{align}
$$
所以$-k=\dfrac{1}{4}$,所以$k=-\dfrac{1}{4}$
题2-2

分母大的反而小
$$
\begin{align}
&n \left( \dfrac{1}{n^2+n}+\dfrac{1}{n^2+n}+\cdots+\dfrac{1}{n^2+n} \right) \nonumber \\
\le&n \left( \dfrac{1}{n^2+1}+\dfrac{1}{n^2+2}+\cdots+\dfrac{1}{n^2+n} \right) \nonumber \\
\le&n \left( \dfrac{1}{n^2+1}+\dfrac{1}{n^2+1}+\cdots+\dfrac{1}{n^2+1} \right) \nonumber \\
\end{align}
$$
$n \left( \dfrac{1}{n^2+n}+\dfrac{1}{n^2+n}+\cdots+\dfrac{1}{n^2+n} \right)=n\dfrac{n}{n^2+n}$
$n \left( \dfrac{1}{n^2+1}+\dfrac{1}{n^2+1}+\cdots+\dfrac{1}{n^2+1} \right)=n\dfrac{n}{n^2+1}$
根据无穷比无穷型极限的求解方法得:
$\lim \limits_{n \to \infty }n\dfrac{n}{n^2+n}=1$
$\lim \limits_{n \to \infty }n\dfrac{n}{n^2+1}=1$
根据数列夹逼准则可得:
$\lim \limits_{n \to \infty }n \left( \dfrac{1}{n^2+1}+\dfrac{1}{n^2+2}+\cdots+\dfrac{1}{n^2+n} \right)=1$
注意审题,前面还有一个n别忘了
题2-3

解:
根据两个无穷小的比较-定义知道:
两个无穷小的比可以是$0$, $\infty $,$1$,常数$C$,所以选B
题2-4

解:选C
初等函数的极限值等于函数值
$\lim \limits_{x \to 1 }\dfrac{sin(x-1)}{x}=\dfrac{sin(1-1)}{1}=\dfrac{0}{1}=0 $正确,排除A
$\lim \limits_{x \to 3^- }(x+1)=3+1=4$正确,排除答案B
$\lim \limits_{x \to 0^+ }\dfrac{1}{x}=+ \infty $
$\lim \limits_{x \to 0^- }\dfrac{1}{x}=- \infty $
指数函数图像
所以$
\lim \limits_{x \to 0^+ }(\dfrac{1}{5})^{\dfrac{1}{x}}
=(\dfrac{1}{5})^{\lim \limits_{x \to 0^+ }\dfrac{1}{x}}
=0
$
$
\lim \limits_{x \to 0^- }(\dfrac{1}{5})^{\dfrac{1}{x}}
=(\dfrac{1}{5})^{\lim \limits_{x \to 0^- }\dfrac{1}{x}}
=+\infty
$
所以$\lim \limits_{x \to 0}(\dfrac{1}{5})^{\dfrac{1}{x}}$不存在,所以这题选C
$\lim \limits_{x \to 0^- }e^{\dfrac{1}{x}}
=e^{ \lim \limits_{x \to 0^- } \dfrac{1}{x}}
=0
$排除D
题2-5

解:
整数指数幂的运算性质:$(a^m)^n=a^{mn}$
$x_2= \sqrt{ax_1}=(ax_1)^{\dfrac{1}{2}}=a^\dfrac{1}{2}x_1^\dfrac{1}{2}$,
$$
\begin{align}
&x_3 \nonumber \\
=&\sqrt{ax_2} \nonumber \\
=&\sqrt{a(ax_1)^{\dfrac{1}{2}}} \nonumber \\
=&(a(ax_1)^{\dfrac{1}{2}})^{\dfrac{1}{2}} \nonumber \\
=&(a(a^\dfrac{1}{2}x_1^\dfrac{1}{2}))^{\dfrac{1}{2}} \nonumber \\
=&a^\dfrac{1}{2}(a^\dfrac{1}{2}x_1^\dfrac{1}{2})^\dfrac{1}{2} \nonumber \\
=&a^\dfrac{1}{2}a^{\dfrac{1}{2}\dfrac{1}{2}}x_1^{\dfrac{1}{2}\dfrac{1}{2}} \nonumber \\
\end{align}
$$
我算错了这题,懒得再往下算了。
题2-6
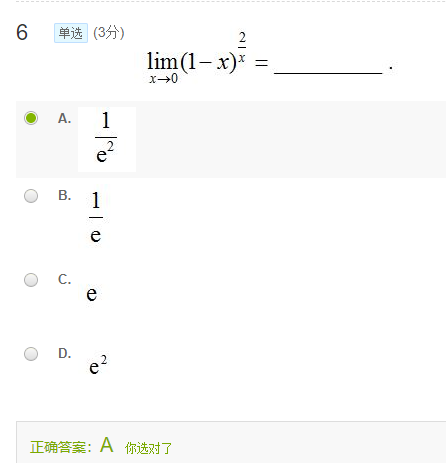
重要的极限:
$\lim \limits_{x \to \infty }(1+\dfrac{1}{x})^x=e$,
$\lim \limits_{x \to 0 }(1+x)^\dfrac{1}{x}=e$
看题目的形式,这里要构造第二中形式。
令$u=-x$,所以$x=-u$,所以$\dfrac{2}{x}= \dfrac{2}{-u}$,同时$x \to 0$,存在$u \to 0$
$$
\begin{align}
&\lim \limits_{x \to 0 }(1-x)^{\dfrac{2}{x}} \nonumber \\
=&\lim \limits_{u \to 0 }(1+u)^{\dfrac{2}{-u}} \nonumber \\
=&\lim \limits_{u \to 0 }(1+u)^{\dfrac{1}{u}-2} \nonumber \\
=&(\lim \limits_{u \to 0 }(1+u)^{\dfrac{1}{u}})^{-2} \nonumber \\
=&e^{-2} \nonumber \\
=&\dfrac{1}{e^2} \nonumber \\
\end{align}
$$
题2-7

解:
$\lim \limits_{x \to 0^+ }f(x)=\lim \limits_{x \to 0^+ }x+1=1$
$$
\begin{align}
&\lim \limits_{x \to 0^- }f(x) \nonumber \\
=&\lim \limits_{x \to 0^- }\dfrac{sinkx}{2x} \nonumber \\
=&\lim \limits_{x \to 0^- }\dfrac{kx}{2x} \nonumber \\
=&\dfrac{k}{2} \nonumber \\
=&1 \nonumber \\
\end{align}
$$
所以$k=2$
题2-8

$x \to 0$时有等价无穷小公式:
$\sqrt[n]{1+x}-1 \sim \dfrac{1}{n}x$
$\sqrt[3]{1-3x}-1 \sim \dfrac{1}{3}-3x=-x$
所以 $\lim \limits_{x \to 0 }\dfrac{\sqrt[3]{1-3x}-1}{x}=\lim \limits_{x \to 0 }\dfrac{-x}{x}=-1$
排除答案C,但是题目没有说函数是否连续,所以不能判断$x=0$函数值a与及极限的关系。
所以a取任意实数。所以选B
题2-9

$$
\begin{align}
&\lim \limits_{x \to 0 }\dfrac{sim(3x^2-x^3)}{x} \nonumber \\
=&\lim \limits_{x \to 0 }\dfrac{3x^2-x^3}{x} \nonumber \\
=&\lim \limits_{x \to 0 }3x-x^2 \nonumber \\
=&0 \nonumber \\
\end{align}
$$
所以是高阶的无穷小
题2-10
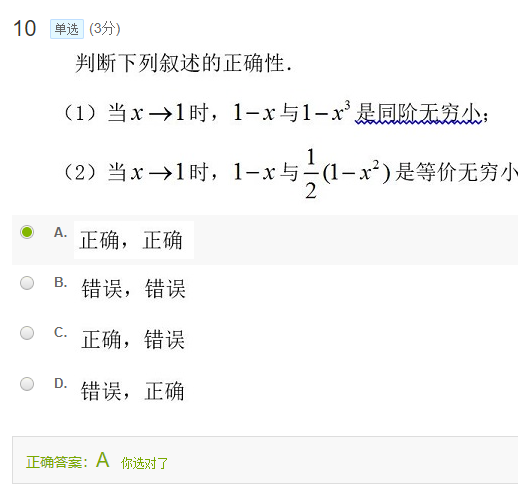
解:
根据立方差公式:$a^3-b^3=(a-b)(a^2+ab+b^2)$
得:$1-x^3=1-x^3=(1-x)(1+x+x^2)$
$$
\begin{align}
&\lim \limits_{x \to 1 }\dfrac{1-x}{1-x^3} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{1-x}{(1-x)(1+x+x^2)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{1}{1+x+x^2} \nonumber \\
=&\dfrac{1}{1+1+1^2} \nonumber \\
=&\dfrac{1}{3} \nonumber \\
\end{align}
$$
所以是同阶无穷小,排除B和D
$$
\begin{align}
&\lim \limits_{x \to 1 }\dfrac{1-x}{\dfrac{1}{2}(1-x^2)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{1-x}{\dfrac{1}{2}(1-x)(1+x)} \nonumber \\
=&\lim \limits_{x \to 1 }\dfrac{1}{\dfrac{1}{2}(1+x)} \nonumber \\
=&\dfrac{1}{\dfrac{1}{2}(1+1)} \nonumber \\
=&\dfrac{1}{1} \nonumber \\
=&1 \nonumber \\
\end{align}
$$
所以是等价的无穷小,正确。
所以选A
本文链接: 第三讲 测验


